Vejamos se alguém sabe como resolver esta questão, estou precisando.....
Postei 2 fotos para entenderem melhor o desenho e o que se pede.
Eu ja fiz a letra A, mas nao conssigo fazer a B.
Na figura abaixo temos uma sucessao de triangulos retangulos em que um de seus catetos mede 1cm. Cada angulo TETAn, onde n=1,2,3,4..... , o n representa o angulo formado pela hipotenusa e um cateto de 1cm. Faça o que se pede:







 , está errado. Isto não é progressão aritmética, é apenas a soma de quadrados. Vai a dica:
, está errado. Isto não é progressão aritmética, é apenas a soma de quadrados. Vai a dica: 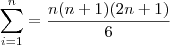 . Usando isso você deve chegar na resposta.
. Usando isso você deve chegar na resposta.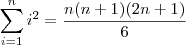 .
. 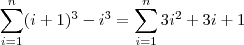
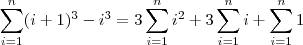
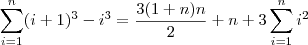
![\sum_{i=1}^n (i+1)^3 - i^3 = (\cancel{2^3} - 1^3) + (\cancel{3^3} - \cancel{2^3}) + (\cancel{4^3} - \cancel{3^3}) + \cancel{\cdots} + [(n+1)^3 - \cancel{n^3}] \sum_{i=1}^n (i+1)^3 - i^3 = (\cancel{2^3} - 1^3) + (\cancel{3^3} - \cancel{2^3}) + (\cancel{4^3} - \cancel{3^3}) + \cancel{\cdots} + [(n+1)^3 - \cancel{n^3}]](/latexrender/pictures/903da68a51eddbc3751a1cac8fae965c.png)
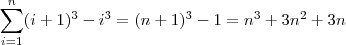
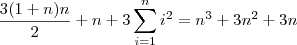
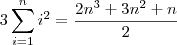
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.