Duvida em perimetro de triangulo

por **bmachado** » Dom Mar 18, 2012 17:39

(Ufu) Na figura a seguir, ABC é um triângulo e
suas medianas AP, BN e CM medem,
respectivamente, 8 cm, 10 cm e 4 cm.Se BQ é paralelo ao lado AC com 2BQ = AC, então,
o perímetro do triângulo APQ é igual a
a) 24 cm. b) 22 cm. c) 20 cm. d) 18 cm.

Obs'n sei postar imagem, favor acesse
Imagem no link:http://www.angloguarulhos.com.br/arquivos/arquivo_2322_20100417204641.pdf

por **LuizAquino** » Seg Mar 19, 2012 00:56

bmachado escreveu:(Ufu) Na figura a seguir, ABC é um triângulo e
suas medianas AP, BN e CM medem,
respectivamente, 8 cm, 10 cm e 4 cm.Se BQ é paralelo ao lado AC com 2BQ = AC, então,

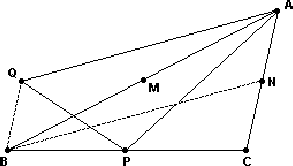
figura.png (2.09 KiB) Exibido 3793 vezes

o perímetro do triângulo APQ é igual a
a) 24 cm. b) 22 cm. c) 20 cm. d) 18 cm.

Como BQ = AC/2, BQ é paralelo a AC e NC = AC/2, temos que BN e AQ são paralelos BN = AQ.

Como N é ponto médio de AC e M é ponto médio de AB, temos que MN é paralelo a BC e MN = BC/2 (ou seja, MN é base média de ABC).

Lembrando que BQ e NC são paralelos e que BQ = NC, temos que Q, M e N são colineares (isto é, estão sobre uma mesma reta). Temos então que QN e BC são paralelos e que QN = BC.

Como MN = BC/2 = PC, temos que QM = BP = PC. Ou seja, QM e PC são paralelos, com QM = PC.

Temos então que PQ é paralelo a CM, com PQ = CM.

Considerando essas informações, tente terminar o exercício.