Pessoal, estou postando esses exercício aqui porque tenho que entregá-los segunda feira, e estous tentando ao máximo resolver sozinho, mas alguns que está difícil chegar a um resultado em tempo hábil. Fiquei o dia todo estudando sobre os números reais e as ''regras'' que devemos seguir nas desigualdades no livro calculo a uma variavel . Enfim, vamos ao exercício. Preciso mostrar que 2 proposições são verdadeiras.
São elas:
(a) Se 1,3 ? x ? 1,4 e 2,8 ? y ? 2,9 , então - 1,6 ? x - y ? - 1,4.
(b) Se 2,9 ? x ? 3 e 1,7 ? y ? 1,8 , então 2,9/1,8 ? x/y ? 3/1,7
Sei que para provar que uma proposição é falta basta exibir um contra exemplo, ou que a hipótese e a tese devem ser igualmente satisfeitas. Mas não sei como aplicar nessas inequações. Se alguem puder dar um caminho, agradeço. Enquanto isso vou tentando aqui... obrigado aeww


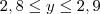 , então
, então 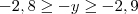 . Ou ainda, podemos escrever que
. Ou ainda, podemos escrever que 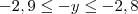 .
.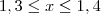 , temos que:
, temos que: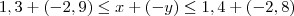

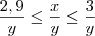
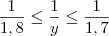
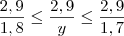
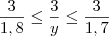
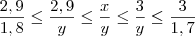
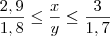


 .
.



