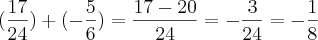
A pergunta é a seguinte: Como faço para saber somente olhando os denominadores das frações, qual é o M.M.C, entre 24 e 6, sem precisar decompor esses dois números em fatores primos!
Qual a maneira para saber qual é o m.m.c entre dois números inteiros, sem precisar decompor em fatores primos, com isso ganhando mais tempo, na hora de resolver contas como essas.
2º pergunta: Qual analogia devo comparar á subtração de frações, para entender o que significa a resposta
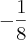.Qual desenho geométrico devo associar essa subtração de frações, para entender a resposta
.
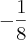no numerador e denominador, e a segunda por 
da mesma forma, teremos 
. Como tem o mesmo denominador, podemos subtrair os numeradores, aí 
.
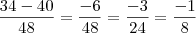por ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.