Bem, eu estou fazendo cursinho pré-vestibular e já terminei o ensino médio.
Mas não dos detalhes, do que fazer e como.
Eu não faço a minima ideia de como resolve, já tentei e não consigo. ='(
Eu sempre tive dificuldade. Interpretar e resolver.
Esta que eu estou com dificuldade, não sei o que fazer com o k :/
Deve ser muito fácil. Lá vai:
O menor valor inteiro de k para que a equação algébrica 2x(kx-4)-x²+6=0 em x não tenha raízes reais é:
a) -1 b)2 c)3 d)4 e)5
fico triste por não lembrar :/
eu quero aprender de novo

por favor me ajude!


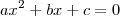
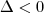 , sendo que
, sendo que 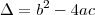 .
.

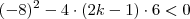

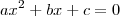 e
e  é diferente de zero, sabemos que são duas soluções e são da forma
é diferente de zero, sabemos que são duas soluções e são da forma 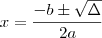 , onde as letras representam os números da equação inicial. Esse símbolo
, onde as letras representam os números da equação inicial. Esse símbolo  denota um outro número auxiliar que ajuda a determinar se ela tem soluções
denota um outro número auxiliar que ajuda a determinar se ela tem soluções 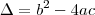 . Se ele for maior que zero, teremos que ela tem duas soluções
. Se ele for maior que zero, teremos que ela tem duas soluções 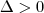 tem duas soluções diferentes,
tem duas soluções diferentes,  tem duas iguais e
tem duas iguais e 
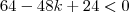
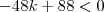
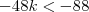
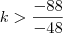
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.