O resultado da simplificação da expressão 7^9+4X7^6+5X7^3+2/344² é
a) 7³ + 2
b)7³ - 4
c)7³ + 5
d) 3
e) 1
Já tentei várias vezes naum sei se tem alguma coisa errada na questão ou algum passo q ainda naum visualizei. Ajudem!!!



Pri Ferreira escreveu:O resultado da simplificação da expressão 7^9+4X7^6+5X7^3+2/344² é
a) 7³ + 2
b)7³ - 4
c)7³ + 5
d) 3
e) 1
Pri Ferreira escreveu:Já tentei várias vezes naum sei se tem alguma coisa errada na questão ou algum passo q ainda naum visualizei.
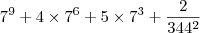
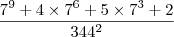
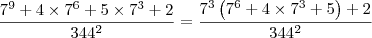
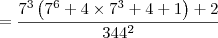
![= \dfrac{7^3\left[ (7^3 + 2)^2 + 1\right] + 2}{344^2} = \dfrac{7^3\left[ (7^3 + 2)^2 + 1\right] + 2}{344^2}](/latexrender/pictures/e3321cc1381e1676b6c4602f7b791595.png)
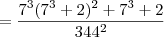
![= \dfrac{\left(7^3 + 2\right)\left[7^3\left(7^3 + 2\right) + 1\right]}{344^2} = \dfrac{\left(7^3 + 2\right)\left[7^3\left(7^3 + 2\right) + 1\right]}{344^2}](/latexrender/pictures/3e6162b472d180bb38edf3e0c11deb7e.png)
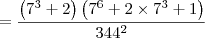
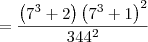
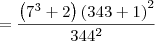
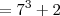

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)