 por Scheu » Sex Mar 16, 2012 00:01
por Scheu » Sex Mar 16, 2012 00:01
Ola! estou começando a aprender a utilização de derivadas, de modo geral a derivação parece fácil, contudo, muitas duvidas estão surgindo. Tenho o seguinte problema para resolver e gostaria de ajuda: " a função
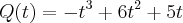
expressa a quantidade de peças produzidas por um operário em t horas, numa fabrica. Determine:
a) a função que da a produção instantânea.
R- "achei" (me disseram) que a resposta é a derivada (
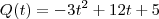
), contudo, gostaria de uma explicação de porque a simples derivação nos leva a achar produção instantânea?
b) para calcular a quantidade de peças produzidas em 2 horas devo simplesmente proceder a resolução da equação? Assim a resposta é:
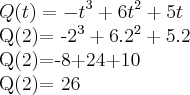
c)Como faço para achar a quantidade Máxima de peças que o operário produz?
Desde já agradeço.
-
Scheu
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Fev 01, 2012 23:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências Contábeis
- Andamento: cursando
 por MarceloFantini » Sex Mar 16, 2012 03:17
por MarceloFantini » Sex Mar 16, 2012 03:17
Se a quantidade de produtos num tempo t, a produção instantânea será dada por
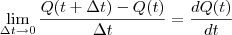
. Ou seja, você pega variações da quantidade de produtos e divide pela variação do tempo. Quando esta variação é muito pequena, ou infinitesimal, diremos que é a derivada.
Se você quer apenas a quantidade de produtos em 2 horas, basta substituir na fórmula original. Porém, se quer a produção deverá substituir na derivada.
Por último, procure rever os teoremas de cálculo que dizem que os possíveis pontos de máximo e mínimo locais de uma função ocorrem quando sua primeira derivada é zero, ou seja
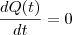
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Aplicacoes de derivadas
 por aline_n » Qui Jun 02, 2011 17:29
por aline_n » Qui Jun 02, 2011 17:29
- 1 Respostas
- 3776 Exibições
- Última mensagem por LuizAquino

Qui Jun 02, 2011 20:34
Cálculo: Limites, Derivadas e Integrais
-
- Aplicações de Derivadas
 por lucasabreuo » Seg Mai 06, 2019 11:56
por lucasabreuo » Seg Mai 06, 2019 11:56
- 2 Respostas
- 5570 Exibições
- Última mensagem por adauto martins

Dom Jul 07, 2019 17:07
Cálculo: Limites, Derivadas e Integrais
-
- derivadas e suas aplicações
por ssousa3 » Sex Mai 27, 2011 18:07
- 11 Respostas
- 8733 Exibições
- Última mensagem por ssousa3

Sáb Mai 28, 2011 22:13
Cálculo: Limites, Derivadas e Integrais
-
- Problema max e mins ( aplicações de derivadas )
 por Nandodtx » Dom Mai 29, 2011 00:17
por Nandodtx » Dom Mai 29, 2011 00:17
- 11 Respostas
- 6893 Exibições
- Última mensagem por LuizAquino

Seg Mai 30, 2011 11:44
Cálculo: Limites, Derivadas e Integrais
-
- [Aplicações Derivadas] Dúvida exerc 1
por MrJuniorFerr » Sáb Out 20, 2012 01:21
- 3 Respostas
- 2636 Exibições
- Última mensagem por Russman

Sáb Out 20, 2012 02:43
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
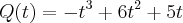 expressa a quantidade de peças produzidas por um operário em t horas, numa fabrica. Determine:
expressa a quantidade de peças produzidas por um operário em t horas, numa fabrica. Determine: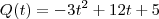 ), contudo, gostaria de uma explicação de porque a simples derivação nos leva a achar produção instantânea?
), contudo, gostaria de uma explicação de porque a simples derivação nos leva a achar produção instantânea?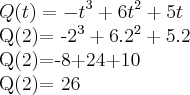


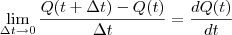 . Ou seja, você pega variações da quantidade de produtos e divide pela variação do tempo. Quando esta variação é muito pequena, ou infinitesimal, diremos que é a derivada.
. Ou seja, você pega variações da quantidade de produtos e divide pela variação do tempo. Quando esta variação é muito pequena, ou infinitesimal, diremos que é a derivada. 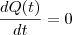 .
.
