Olá pessoal.
Tenho dúvida nesta questão:
Um retângulo com lados adjacentes medindo Sen a e Cos b, com 0 < a ?/2, tem Perímetro igual a ?6. Qula a área do retângulo?
bom; O perímetro é a soma de todos os lados do retângulo
A área é a fórmula base x altura.
Pois não consegui chegar a um resultado conforme marcada pela questão: 1/4
Ficarei grato pela ajuda


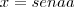 e
e 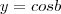 ou inverso, o que estaríamos fazendo é trocar a referência do ângulo
ou inverso, o que estaríamos fazendo é trocar a referência do ângulo  para o ângulo
para o ângulo  , veja a figura.
, veja a figura.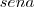 e o outro o
e o outro o 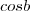 ,
,  é igual ao ângulo
é igual ao ângulo  . Isto é:
. Isto é: daí decorre que o perímetro é igual a
daí decorre que o perímetro é igual a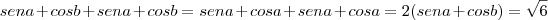 , ou seja:
, ou seja: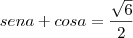 , elevemos ao quadrado ambos os membros dessa igualdade:
, elevemos ao quadrado ambos os membros dessa igualdade: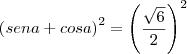 , que desenvolvendo dá:
, que desenvolvendo dá: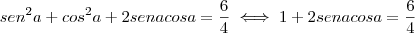
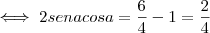 . Então
. Então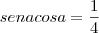 que é a área pedida (
que é a área pedida ( 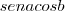 ).
).