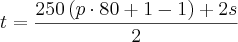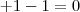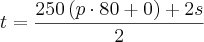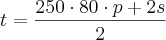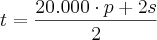Seção para postagens de problemas matemáticos do cotidiano, reportagens, casos interessantes, polêmicos ou curiosos.
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por admin » Qua Fev 27, 2008 11:57
por admin » Qua Fev 27, 2008 11:57
1- Digite os 4 primeiros algarismos de seu telefone (não vale número de celular);
2- multiplique por 80;
3- some 1;
4- multiplique por 250;
5- some com os 4 últimos algarismos do mesmo telefone;
6- some com os 4 últimos algarismos do mesmo telefone novamente;
7- subtraia 250;
8- divida por 2.
Reconhece o resultado?
É o número completo de seu telefone!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por admin » Qua Fev 27, 2008 12:16
por admin » Qua Fev 27, 2008 12:16
A explicação é simples.
De imediato, suspeitamos que a seqüência de operações leva à uma expressão como esta:
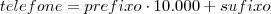
Pois o prefixo possui 4 dígitos e após multiplicarmos por
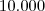
, teremos um número como "
prefixo0000" que somado com o sufixo ficará "
prefixosufixo".
Resta apenas confirmar, unindo as operações em uma única expressão, respeitando a precedência.
telefone: t
prefixo: p
sufixo: s
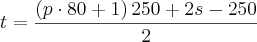
Colocando
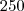
em evidência:
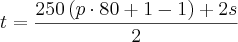
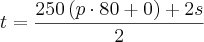
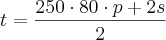
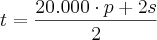
Dividindo as duas parcelas por 2:


Que, de fato, é a expressão esperada.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
Voltar para Problemas do Cotidiano
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


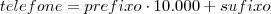
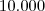 , teremos um número como "
, teremos um número como "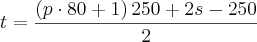
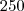 em evidência:
em evidência: