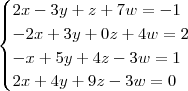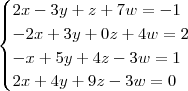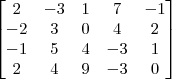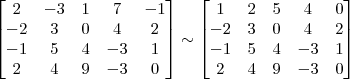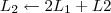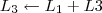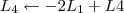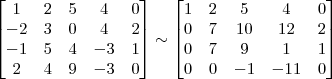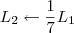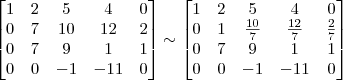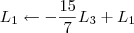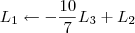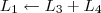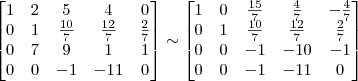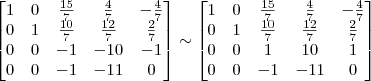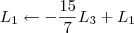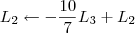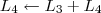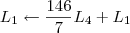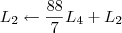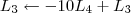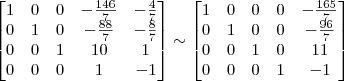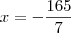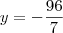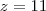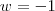por Claudin » Seg Fev 27, 2012 18:04
por Claudin » Seg Fev 27, 2012 18:04
Não sei se o resultado a seguir está correto, alguém ajuda?
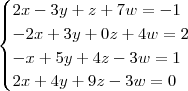
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Sáb Mar 03, 2012 23:17
por LuizAquino » Sáb Mar 03, 2012 23:17
Claudin escreveu:Não sei se o resultado a seguir está correto, alguém ajuda?
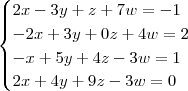
Claudin escreveu: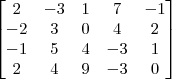 1º Passo
1º Passo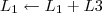
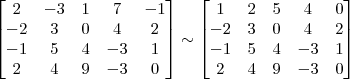 2º Passo
2º Passo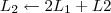
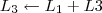
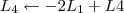
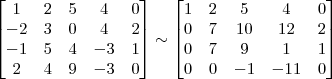 3º Passo
3º Passo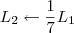
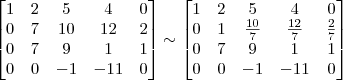 4º Passo
4º Passo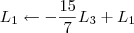
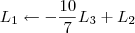
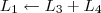
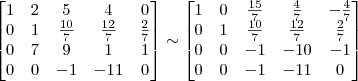 5º Passo
5º Passo
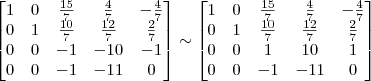 6º Passo
6º Passo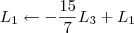
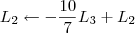
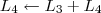
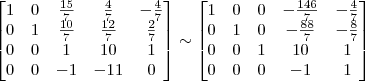 7º Passo
7º Passo
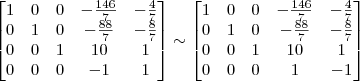 8º Passo
8º Passo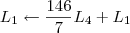
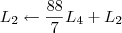
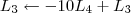
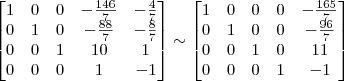
Você sabe conferir a solução de um sistema de equações?
Por exemplo, considere o sistema abaixo:
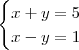
Se for afirmado que a solução desse sistema é x = 3 e y = 2, você sabe conferir se isso é verdade?
Pois bem, se você souber fazer isso, então você pode conferir se a solução do sistema que você tentou resolver é:
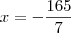
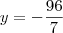
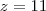
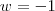
Caso você não saiba como conferir a solução de um sistema, basta informar isso em sua próxima mensagem. Nesse caso, eu explicarei como proceder.
Por fim, eu aproveito para lhe dar uma dica. No
WolframAlpha você pode escalonar uma matriz pelo método de Gauss-Jordam. Para isso, siga os passos:
- acesse a página WolframAlpha;
- no campo de entrada, digite o comando:
- Código: Selecionar todos
row reduce {{2, -3, 1, 7, -1}, {-2, 3, 0, 4, 2}, {-1, 5, 4, -3, 1}, {2, 4, 9, -3, 0}}
- clique no botão "=";
- aguarde a página ser carregada;
- ao lado do resultado apresentado, clique no botão "Show steps";
- Pronto! Basta você comparar a sua resolução com a que for apresentada na página.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [MATRIZ] Como acho o determinante dessa matriz
por LAZAROTTI » Qui Mai 03, 2012 00:38
- 4 Respostas
- 7173 Exibições
- Última mensagem por Russman

Qui Mai 03, 2012 01:56
Matrizes e Determinantes
-
- [Matriz]- inversa de uma matriz
por Ana_Rodrigues » Seg Mar 26, 2012 08:54
- 2 Respostas
- 3576 Exibições
- Última mensagem por Ana_Rodrigues

Seg Mar 26, 2012 18:05
Matrizes e Determinantes
-
- [MATRIZ]Determinante da Matriz 4x4
por LAZAROTTI » Qui Mai 03, 2012 22:33
- 1 Respostas
- 6730 Exibições
- Última mensagem por LuizAquino

Sex Mai 11, 2012 08:00
Matrizes e Determinantes
-
- [Matriz] Matriz com potencias
por rochadapesada » Dom Abr 07, 2013 20:29
- 3 Respostas
- 4705 Exibições
- Última mensagem por DanielFerreira

Seg Abr 08, 2013 17:32
Matrizes e Determinantes
-
- matriz
por Barbara » Ter Ago 18, 2009 15:26
- 4 Respostas
- 4817 Exibições
- Última mensagem por Molina

Qui Ago 20, 2009 18:11
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.