(FEI-MAUÁ-SP)Resolver a inequação (2x + 1)/(x - 3) ? 1
Bom, tentei resolver isso de tudo qualquer jeito, mas não consegui. Fiz duas tentativas:
1ª tentativa
Chamei 2x + 1 de f(x) e igualei a zero, e x - 3 de g(x) e fiz o mesmo:
f(x) = 2x + 1
0 = 2x + 1
x = -1/2
g(x) = x - 3
0 = x - 3
x = 3
Depois coloquei na reta da função f o valor de -1/2 e na outra reta paralela a f a reta g e coloquei o 3. E depois fiz o jogo dos sinais:
Para que a inequação seja ? 0, então x ? -1/2 ou x> 3
Portanto, o conjunto solução é: S = {x??| x ? -1/2 ou x > 3}
Mas não faz sentido x ser ? 0, pois a inequação pede os valores de x para que seja ? 1.
Então fiz a 2ª tentativa:
(2x+1)/(x-3) ? 1 --> multiplique "em cruz"
2x+1 ? x-3
2x-x+1+3 ? 0
x + 4 ? 0
x ? -4
Não podemos esquecer também que x tem que ser diferente de 3, pois o denominador não pode ser 0 né.
Mas como vou saber se x vai ser x > 3 ou x < 3?
E mesmo assim está errado x ? -4, pois a resposta correta é:
S = {x??|x ? -4 ou x > 3}
Gostaria que me falasse onde que errei e como saber se o x é x > 3 ou x < 3
Ufa! escrevi um livro
Agradeço desde já


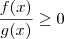 .
.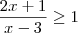
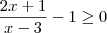
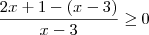
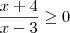

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.