 por Rosana Vieira » Sex Mar 02, 2012 00:52
por Rosana Vieira » Sex Mar 02, 2012 00:52
Estou com duvida para resolver este exercício se alguem poder me ajudar eu agradeço
Considere uma PG constituída de números positivos {a1, a2...}, e a partir daí consideremos uma nova sequência dos respectivos logaritmos dos elementos da progressão geométrica dada, tomados em uma base b, tal que 0 < b ? 1.
Mostre que essa nova sequência é uma PA.
-
Rosana Vieira
- Usuário Parceiro

-
- Mensagens: 74
- Registrado em: Qui Nov 17, 2011 00:11
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por timoteo » Sex Mar 02, 2012 02:52
por timoteo » Sex Mar 02, 2012 02:52
rosana, vamos ver se eu entendi bem.
pegando o termo geral da P.G. temos:
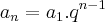
colocando os dois lados no logaritmo de base b ficamos:
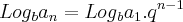
= n-1

= (n-1) x + y = t. lembrando que toda equaçao do primeiro grau é uma P.A. temos : (n-1) x + y

az + b = r.
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
Voltar para Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


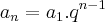 colocando os dois lados no logaritmo de base b ficamos:
colocando os dois lados no logaritmo de base b ficamos: 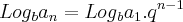 = n-1
= n-1 = (n-1) x + y = t. lembrando que toda equaçao do primeiro grau é uma P.A. temos : (n-1) x + y
= (n-1) x + y = t. lembrando que toda equaçao do primeiro grau é uma P.A. temos : (n-1) x + y  az + b = r.
az + b = r.

 .
.



