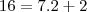Fração continua

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Fração continua

Regras do fórum
Responder

Fração continua

Mensagempor Rosana Vieira » Sex Mar 02, 2012 00:48

Como eu faço para resolver a fração continua com fração 16/7.
Rosana Vieira
Usuário Parceiro
Usuário Parceiro
 
Mensagens: 74
Registrado em: Qui Nov 17, 2011 00:11
Formação Escolar: PÓS-GRADUAÇÃO
Área/Curso: Matemática
Andamento: cursando
Voltar ao topo

Re: Fração continua

Mensagempor timoteo » Sex Mar 02, 2012 02:09

rosana, faça o seguinte: utilizando o algoritmo de euclides divida a fraçao. 16 = 7 . 2 + 2 agora divida todos por 7 e obteremos 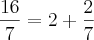\frac{16}{7} = 2 + \frac{2}{7}. supondo que vc ja saiba a estrutura da representaçao de um fraçao continuada, tremos: 2 + 2/7 transformando a fraçao temos: 2 + 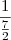\frac{1}{\frac{7}{2}}, efetuando a divisao e invertendo vamos encontrar como ultimo numerador da ultima fraçao o nemro 1. teremos: 2 + \frac{1}{3 + \frac{1}{2}}.

onde o primeiro termo 2 pertence ao inteiros e os demais numeros sao inteiros positivos.

o mais interresante é que essa é uma forma diferente de representar numeros. essa maneira peculiar de representaçao tem umapropriedade interresante onde se a divisao for infinita o numero é irracional e se for limitada como nesse caso teremos um numero racional.

a rrepresentaçao mais apropriada é: [2;3,2]
timoteo
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 117
Registrado em: Ter Fev 14, 2012 07:07
Formação Escolar: GRADUAÇÃO
Área/Curso: bacharel matemática
Andamento: cursando
Voltar ao topo
Responder

Voltar para Álgebra Elementar

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

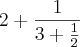Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 


Tópico Popular

Assunto: Taxa de variação
Autor: felipe_ad - Ter Jun 29, 2010 19:44

Como resolvo uma questao desse tipo:

Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?

A letra (a) consegui resolver e cheguei no resultado correto de \frac{4\pi{r}^{2}}{3}
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é 1,066\pi

Alguem me ajuda? Agradeço desde já.

Assunto: Taxa de variação
Autor: Elcioschin - Qua Jun 30, 2010 20:47

V = (1/3)*pi*r²*h ----> h = 4r/3

V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³

Derivando:

dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3

Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s

Assunto: Taxa de variação
Autor: Guill - Ter Fev 21, 2012 21:17

Temos que o volume é dado por:

V = \frac{4\pi}{3}r^2


Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

\frac{dV}{dt} = \frac{8\pi.r}{3}.\frac{dr}{dt}


Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:

\frac{dV}{dt} = \frac{8\pi.2}{3}.\frac{2}{10}

\frac{dV}{dt} = \frac{16\pi}{15}

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum