 por Aline » Ter Abr 28, 2009 14:26
por Aline » Ter Abr 28, 2009 14:26
oiii, estou com dificuldades para resolver este exercicio de pa pois não consigo identificar os termos dela...
Determinar o ultimo termo da pa (9,6,3....an) sabendo que a soma de seus elementos é -12.
-
Aline
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Abr 22, 2009 18:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por Marcampucio » Ter Abr 28, 2009 18:03
por Marcampucio » Ter Abr 28, 2009 18:03
Soma da PA:
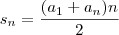
Enésimo termo:

tratando como um sistema a duas incógnitas:
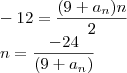

resolvendo a equação temos
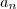
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por Cleyson007 » Qua Jun 10, 2009 12:48
por Cleyson007 » Qua Jun 10, 2009 12:48
Olá Aline!
Primeiramente, seja bem-vinda ao Ajuda Matemática.
Quanto a explicação do exercício:
Fórmulas:

(Fórmula do Termo Geral

)
Soma dos termos da P.A -->
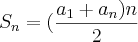
Note que na questão estão faltando dois dados:

e

.
Vamos procurar

-->
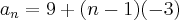
(Note que a razão é negativa, decrescente).
Logo,
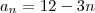
.
Substituindo o valor de

em
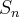
, encontramos:
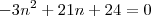
Resolvendo:
 Portanto:
Portanto: 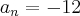
Comente qualquer dúvida

Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



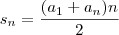

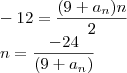

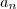

 (Fórmula do Termo Geral
(Fórmula do Termo Geral  )
)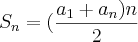
 e
e  .
. -->
--> 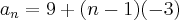 (Note que a razão é negativa, decrescente).
(Note que a razão é negativa, decrescente).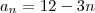 .
. em
em 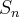 , encontramos:
, encontramos: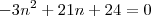

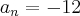



 .
.



