Ola,
Gostaria de uma ajuda na resolução de um problema.
A partir do grafico de uma equação do segundo grau, como posso voltar para equação.
Exemplo: O Grafico de uma equação do segundo grau, toca o eixo do X em 0 (zero) e 240, e tem ponto maximo de 120. Ache a equação.


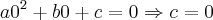
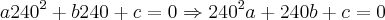
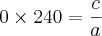
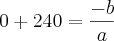
 :
:



 .
.



