 por lendersonfisica » Sex Fev 24, 2012 17:32
por lendersonfisica » Sex Fev 24, 2012 17:32
]Olá. Boa tarde. Gostaria que alguem me ajuda-se a desenvolver uma explicação bem detalhada da questão a seguir, utilizando as coordenadas polares para analisar a existência do limite no ponto (0,0);
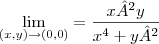
Obrigado Estou aguardando respostas. E tambem tentando desenvolver a questão.
Desde já Grato.
By: Lenderson Francisco Pedro José Souza da Silva
-
lendersonfisica
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Fev 24, 2012 17:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por LuizAquino » Sáb Fev 25, 2012 20:02
por LuizAquino » Sáb Fev 25, 2012 20:02
lendersonfisica escreveu:Gostaria que alguem me ajuda-se a desenvolver uma explicação bem detalhada da questão a seguir, utilizando as coordenadas polares para analisar a existência do limite no ponto (0,0);
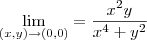
Eu presumo que o limite seja:
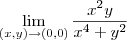
Note que você escreveu o símbolo "=" em um local inadequado.
Como você já deve ter feito, primeiro você precisa transferir esse limite para as coordenadas polares. Para isso, basta utilizar
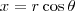
,
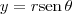
e fazer r tender para 0.
Temos então que:
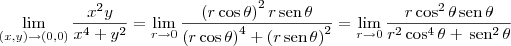
Agora basta escolher dois caminhos para os quais o limite seja distinto.
Escolha por exemplo o caminho tal que os pontos se aproximam de (0, 0) pela reta polar

.
Em seguida, escolha o caminho tal que os pontos se aproximam de (0, 0) pela espiral

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por lendersonfisica » Dom Fev 26, 2012 11:05
por lendersonfisica » Dom Fev 26, 2012 11:05
Presumio Corretamente amigo!
Muito obrigado foi de muita ajuda, para intender uma questão que me foi passada para explicar na aula.
-
lendersonfisica
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Fev 24, 2012 17:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Vetores ! Por favor, da forma mais detalhada possível.Grato
por johnatta » Sáb Mai 23, 2015 11:08
- 0 Respostas
- 0 Exibições
- Última mensagem por Visitante

Qua Dez 31, 1969 22:00
Geometria Analítica
-
- Vetores ! Por favor, da forma mais detalhada possível.Grato
por johnatta » Sáb Mai 23, 2015 12:45
- 0 Respostas
- 1130 Exibições
- Última mensagem por johnatta

Sáb Mai 23, 2015 12:45
Geometria Analítica
-
- Limite Continuidade
por Claudin » Sáb Out 01, 2011 11:33
- 10 Respostas
- 5805 Exibições
- Última mensagem por Claudin

Seg Out 03, 2011 10:37
Cálculo: Limites, Derivadas e Integrais
-
- Continuidade Limite
por CaioLemos » Qui Mar 22, 2012 13:18
- 2 Respostas
- 2016 Exibições
- Última mensagem por CaioLemos

Qui Mar 22, 2012 17:39
Cálculo: Limites, Derivadas e Integrais
-
- Limite e Continuidade
por Thyago Quimica » Seg Mai 21, 2012 14:11
- 1 Respostas
- 1665 Exibições
- Última mensagem por LuizAquino

Ter Mai 22, 2012 19:22
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
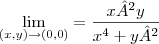

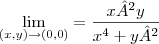

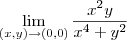
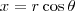 ,
, 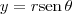 e fazer r tender para 0.
e fazer r tender para 0.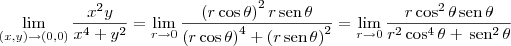
 .
. .
.



 , avisa que eu resolvo.
, avisa que eu resolvo.

