 por Matheus Lacombe O » Sex Fev 24, 2012 11:23
por Matheus Lacombe O » Sex Fev 24, 2012 11:23
-
Matheus Lacombe O
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Sex Jun 03, 2011 22:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecânica
- Andamento: cursando
 por MarceloFantini » Sex Fev 24, 2012 12:55
por MarceloFantini » Sex Fev 24, 2012 12:55
Vou multiplicar tudo por 10 e vejamos como a equação fica:
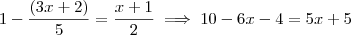
.
Daí,
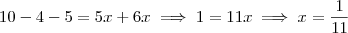
.
Você esqueceu de distribuir o sinal na primeira fração.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Neperiano » Sex Fev 24, 2012 13:10
por Neperiano » Sex Fev 24, 2012 13:10
Ola
Outro forma de resolver
1 - ((3x+2)/5) = (x+1)/2
passa o 2 pro lado
2+((-6x-4)/5)=x+1
passa o 2 pro outro lado
(-6x-4)/5=x-1
passa o 5 pro outro lado
-6x-4=5x-5
isola o x
1=11x
x = 1/11
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [equação modular] resultado confuso
por jvabatista » Qua Abr 18, 2012 02:05
- 2 Respostas
- 1581 Exibições
- Última mensagem por jvabatista

Qua Abr 25, 2012 23:22
Álgebra Elementar
-
- [Resolvido][Equação] Com fração.
por replay » Sex Mar 01, 2013 17:02
- 2 Respostas
- 1087 Exibições
- Última mensagem por replay

Sex Mar 01, 2013 19:25
Álgebra Elementar
-
- Equação Logaritmica com fração
por Rangelgec » Ter Dez 01, 2015 15:59
- 1 Respostas
- 5342 Exibições
- Última mensagem por Gebe

Ter Dez 08, 2015 02:15
Logaritmos
-
- equação do segundo grau com fração
por hevhoram » Sex Abr 20, 2012 12:08
- 1 Respostas
- 3707 Exibições
- Última mensagem por Cleyson007

Sex Abr 20, 2012 12:30
Sistemas de Equações
-
- Como montar a equação contendo Fração e porcentagem
por macedo1967 » Sáb Set 23, 2017 14:16
- 3 Respostas
- 12964 Exibições
- Última mensagem por DanielFerreira

Dom Out 08, 2017 20:20
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
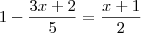


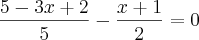
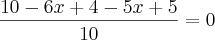


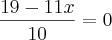
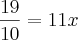
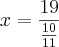

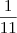


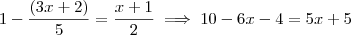 .
.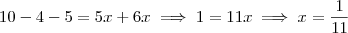 .
.


