Esse método é o cálculo da derivada usando a própria definição. Contudo, não é um método prático e, na maioria dos cálculos, a gente usa outras formas para calcular. Nesse caso, como você citou, poderia usar a regra da potência (
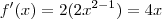
). O que vale salientar é que todas as regras de cálculo são dedutíveis a partir da definição, inclusive o
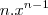
como você pode observar nesse problema.
De qualquer forma, após você encontrar a função derivada, substitui-se o valor de

para o qual é pedida a derivada.
Quanto ao

, trata-se do pequeno incremento que adicionamos a x para efeito de aplicação da definição. Em alguns livros você encontrará

no lugar de

, o que importa é que independente do símbolo usado esse valor é o incremento infinitesimal que se aplica a

e portanto é um valor muito pequeno. Os bons livros de cálculo trazem isso, em geral, de forma mais detalhada.


 , então você estava derivando
, então você estava derivando  . Você pode proceder da mesma forma para
. Você pode proceder da mesma forma para 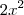 . Perceba que a única diferença é o coeficiente de
. Perceba que a única diferença é o coeficiente de 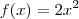 , estamos querendo
, estamos querendo 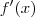 que pela definição é:
que pela definição é: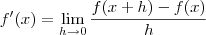
 por
por  e
e  por
por 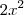 , assim:
, assim: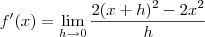
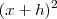 que é igual a
que é igual a 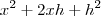 , então:
, então: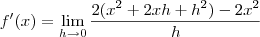 que desenvolvendo fica assim:
que desenvolvendo fica assim: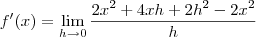 , cancelamos
, cancelamos  em evidência:
em evidência: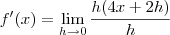 ,
, 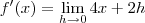 . Se h tende a 0 então 2h também tende a 0 e, no limite, 2h = 0.
. Se h tende a 0 então 2h também tende a 0 e, no limite, 2h = 0.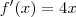 .
.
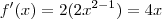 ). O que vale salientar é que todas as regras de cálculo são dedutíveis a partir da definição, inclusive o
). O que vale salientar é que todas as regras de cálculo são dedutíveis a partir da definição, inclusive o 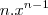 como você pode observar nesse problema.
como você pode observar nesse problema. para o qual é pedida a derivada.
para o qual é pedida a derivada.  no lugar de
no lugar de 
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.