Oi, preciso de ajuda...
z^2-(2+i)z+2i=0
Obrigada
por Camila Z » Dom Fev 19, 2012 11:04
por fraol » Dom Fev 19, 2012 21:30
e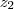 
as raízes dessa equação, 
( o fator de 
), 
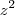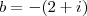( o fator de 
) e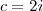 
( o termo independent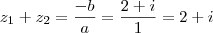e ).
e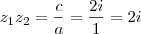 
.
e cujo produto é 
.
por Camila Z » Dom Fev 19, 2012 21:52
por fraol » Dom Fev 19, 2012 22:12
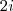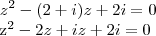
Camila Z escreveu:Mas se eu fizer com a forma básica de 2° grau, dá esses valores tb?
Ainda não vi esses outros jeitos que vc falou, estou no início...
Não sei quem é a, b e c..., com certeza estou pensando errado...
, 
e 
.por Camila Z » Dom Fev 19, 2012 22:18
por fraol » Dom Fev 19, 2012 22:41
Camila Z escreveu:Então... ocorre que não sei fazer isso...
sim, eu vi os valores que vc colocou, mas me confundo para trabalhar com eles... calculo o delta e tudo?
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)