Victor_tnk escreveu:A função real f(x) =
![\frac{2x}{\sqrt[2]{x^2-2x+1}+{\sqrt[2]{x^2+2x+1}}} \frac{2x}{\sqrt[2]{x^2-2x+1}+{\sqrt[2]{x^2+2x+1}}}](/latexrender/pictures/482a22d14c55b2a2aa11758254de7217.png)
tem domínio de validade igual a:
a) R
b) R, exceto {1}
c) R, exceto{-1}
d)R, exceto{-1,1}
e)R+
Victor_tnk escreveu:bom pelas minhas contas percebi que há dois trinômios quadrados perfeitos:
![\frac{2x}{\sqrt[2]{(x+1)^2}+\sqrt[2]{(x-1)^2}} \frac{2x}{\sqrt[2]{(x+1)^2}+\sqrt[2]{(x-1)^2}}](/latexrender/pictures/844635c42d94410163759d250c685d44.png)
Ok.
Victor_tnk escreveu:Usei a condição de existência :
![{\sqrt[2]{(x+1)^2}+\sqrt[2]{(x-1)^2}} \neq 0 {\sqrt[2]{(x+1)^2}+\sqrt[2]{(x-1)^2}} \neq 0](/latexrender/pictures/0e20540309add602e283f295b82a7295.png)
e em seguida os deixei na forma de módulo :
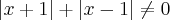
Na verdade, como temos a presença de raízes quadradas, as expressões que aparecem dentro delas não podem ser negativas. Ou seja, devemos ter as condições:
(i)
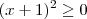
(ii)
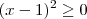
Por outro lado, não pode haver uma expressão nula no denominador. Então precisamos também da condição:
(iii)
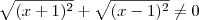
Note que os números
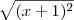
e
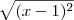
são sempre positivos. Portanto, para que sua soma seja igual a zero, seria necessário que esses dois números fossem zero. Entretanto, não há número real x que faça com que os números
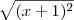
e
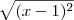
sejam ambos iguais a zero. Conclusão: não importa o valor do número real x, sempre teremos a condição (iii) atendida.
Dessa forma, precisamos nos preocupar apenas com as condições (i) e (ii).
Agora tente concluir o exercício.
![\frac{2x}{\sqrt[2]{x^2-2x+1}+{\sqrt[2]{x^2+2x+1}}} \frac{2x}{\sqrt[2]{x^2-2x+1}+{\sqrt[2]{x^2+2x+1}}}](/latexrender/pictures/482a22d14c55b2a2aa11758254de7217.png) tem domínio de validade igual a:
tem domínio de validade igual a:![\frac{2x}{\sqrt[2]{(x+1)^2}+\sqrt[2]{(x-1)^2}} \frac{2x}{\sqrt[2]{(x+1)^2}+\sqrt[2]{(x-1)^2}}](/latexrender/pictures/844635c42d94410163759d250c685d44.png)
![{\sqrt[2]{(x+1)^2}+\sqrt[2]{(x-1)^2}} \neq 0 {\sqrt[2]{(x+1)^2}+\sqrt[2]{(x-1)^2}} \neq 0](/latexrender/pictures/0e20540309add602e283f295b82a7295.png)
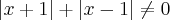
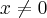 o que não bateu com nenhuma das respostas..
o que não bateu com nenhuma das respostas..

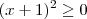
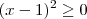
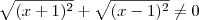
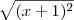 e
e 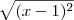 são sempre positivos. Portanto, para que sua soma seja igual a zero, seria necessário que esses dois números fossem zero. Entretanto, não há número real x que faça com que os números
são sempre positivos. Portanto, para que sua soma seja igual a zero, seria necessário que esses dois números fossem zero. Entretanto, não há número real x que faça com que os números 
![\sqrt[2]{(x+1)^2} + \sqrt[2]{(x-1)^2} \sqrt[2]{(x+1)^2} + \sqrt[2]{(x-1)^2}](/latexrender/pictures/187ce45950426707f88b999336063307.png)
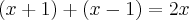 (denominador)
(denominador) 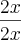 , sendo o domínio podendo assumir qualquer numero real menos 0..
, sendo o domínio podendo assumir qualquer numero real menos 0..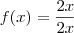 , sendo o domínio podendo assumir qualquer numero real menos 0..
, sendo o domínio podendo assumir qualquer numero real menos 0..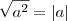 .
.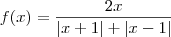

 .
.
 :
: