Luiz Felipe escreveu:Olá, sou novo no fórum, estou fazendo cursinho e vim em busca de algum site que me ajudase em alguns problemas de matemática pois sou muito ruim na materia.
Seja bem vindo ao fórum!
Luiz Felipe escreveu:Tentei utilizar o LaTeX para mostrar como eu tentei resolver as questões, mas iria demorar muito tempo e nesse tempo eu poderia estar fazendo outras questões ou estudando outras matérias, espero que entendam o meu lado, se eu cometi algum erro neste fórum me perdoem pois não sei como funciona direito ainda (...)
Eu entendo o seu ponto de vista.
Mas pare um pouco para pensar: se a pessoa que está lhe ajudando pode "perder" o precioso tempo dela para digitar a resposta em LaTeX, por que você que está querendo a ajuda não pode "perder" também?
Em relação aos exercícios, eu vou exibir o início de cada um deles e você tenta finalizar.
Luiz Felipe escreveu:1° - Determine valores x para os quais a distância entre os pontos A(x + 2, - 3) e B(3, x - 3) é 5.
Aplicando a fórmula de distância entre pontos:
![\sqrt{[(x+2) - 3]^2 + [-3 - (x-3)]^2} = 5 \sqrt{[(x+2) - 3]^2 + [-3 - (x-3)]^2} = 5](/latexrender/pictures/04ce04db0737b15197eba4f17cc8600f.png)
![\left[\sqrt{(x- 1)^2 + (-x)^2}\right]^2 = 5^2 \left[\sqrt{(x- 1)^2 + (-x)^2}\right]^2 = 5^2](/latexrender/pictures/9e389387fbd1a02b98b39eac037e901b.png)
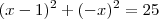
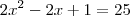
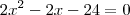
Agora tente terminar a partir daqui.
Luiz Felipe escreveu:2° - Calcule o perimetro do triângulo ABC, sendo A(1, 1), B(2, 2) e C(3, -1).
O perímetro de uma figura é a soma das medidas de seus lados.
Desse modo, para calcular o perímetro basta aplicar a fórmula de distância entre pontos:
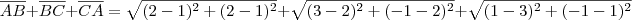
Agora tente continuar a partir daí.
Luiz Felipe escreveu:3º - Os Pontos A(3, 4) e B(1, -2) são equidistantes de P(0, y).Determine y.
Temos que
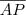
e
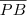
possuem a mesma medida, já que A e B são equidistantes de P.
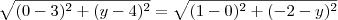
![\left[\sqrt{9 + (y-4)^2}\right]^2 = \left[\sqrt{1 + (-2-y)^2}\right]^2 \left[\sqrt{9 + (y-4)^2}\right]^2 = \left[\sqrt{1 + (-2-y)^2}\right]^2](/latexrender/pictures/b1e48bcc4bf3402bbe08aa4e5a325e97.png)

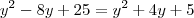
Agora tente continuar a partir daí.
Luiz Felipe escreveu:4° - Qual ponto da segunda Bissetriz é equidistante de P(1, 4) e Q(2, -5).
Está faltando no enunciado da questão a informação sobre qual bissetriz considerar. A julgar pelo gabarito, deseja-se a bissetriz dos quadrantes pares.
Nesse caso, um ponto sobre essa bissetriz tem o formato B = (x, -x).
Como esse ponto deve ser equidistante de P e Q, temos que

.
![\sqrt{(x-1)^2 + (-x-4)^2} = \sqrt{(2-x)^2 + [-5-(-x)]^2} \sqrt{(x-1)^2 + (-x-4)^2} = \sqrt{(2-x)^2 + [-5-(-x)]^2}](/latexrender/pictures/2ed36113a54fa2395866f4572ffeb7e9.png)
![\left[\sqrt{(x-1)^2 + (-x-4)^2}\right]^2 = \left[\sqrt{(2-x)^2 + (-5+x)^2}\right]^2 \left[\sqrt{(x-1)^2 + (-x-4)^2}\right]^2 = \left[\sqrt{(2-x)^2 + (-5+x)^2}\right]^2](/latexrender/pictures/f686b9294d60060cee02cf5a0efc7373.png)

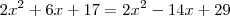
Luiz Felipe escreveu:5° - Qual é a condição para que o ponto (x, 3) seja equidistante dos eixos coordenados.
Se o ponto (x, y) é equidistante dos eixos coordenados, então
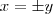
. Usando essa informação, fica fácil concluir o exercício.
Luiz Felipe escreveu: 6° - Qual a condição para que P(x, y) seja equidistante de A(2, 3) e B(5, -1).
Para que seja equidistante, devemos ter

.
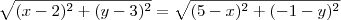
![\left[\sqrt{(x-2)^2 + (y-3)^2}\right]^2 = \left[\sqrt{(5-x)^2 + (-1-y)^2}\right]^2 \left[\sqrt{(x-2)^2 + (y-3)^2}\right]^2 = \left[\sqrt{(5-x)^2 + (-1-y)^2}\right]^2](/latexrender/pictures/7491e548d11b7a23d1af6c23fa50bb65.png)
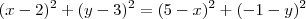

Continue a partir daí.
Luiz Felipe escreveu:7° - Determine as coordenadas do centro C da circunferência que passa pelos pontos P(3, 4) e R(1, -2).
Primeiro, dados dois pontos distintos existem infintas circunferências passando por eles. Sendo assim, haverá infinitas possibilidades para o ponto C.
Portanto, está faltando informação nesse exercício para que seja calculado apenas um C.
De qualquer modo, em todas as possibilidades deve ocorrer

(já que a distância do centro de uma circunferência até qualquer um de seus pontos é sempre igual. Além disso, chamamos essa distância de raio.).
Considerando então C=(x, y), temos que:
![\sqrt{(x-3)^2 + (y-4)^2} = \sqrt{(x-1)^2 + [y-(-2)]^2} \sqrt{(x-3)^2 + (y-4)^2} = \sqrt{(x-1)^2 + [y-(-2)]^2}](/latexrender/pictures/a9bfd1308a51a0f1eb3b6236dae8b3db.png)
![\left[\sqrt{(x-3)^2 + (y-4)^2}\right]^2 = \left[\sqrt{(x-1)^2 + (y+2)^2}\right]^2 \left[\sqrt{(x-3)^2 + (y-4)^2}\right]^2 = \left[\sqrt{(x-1)^2 + (y+2)^2}\right]^2](/latexrender/pictures/3b03d45d94ea556b3a14904069fc9587.png)

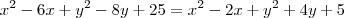
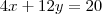
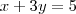
Atribuindo valores para x, obtemos o valor para y. Note que para x = 13/14, temos que y = 19/14.
ObservaçãoComo já lembrou o colega
MarceloFantini, evite enviar mais de um exercício por tópico. Isso prejudica a organização do fórum.
Além disso, vale frisar que não é objetivo do fórum resolver listas de exercício. A nossa ideia básica é tirar dúvidas.
Por fim, para também ajudar nos seus estudos eu recomendo o canal do Nerkie:
http://www.youtube.com/nerckie![(3 + \sqrt[]{5}) \sqrt[]{2} (3 + \sqrt[]{5}) \sqrt[]{2}](/latexrender/pictures/2959e92edd6a7740f7ea512818e038af.png)

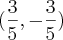
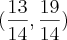




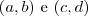 é
é 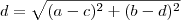 , é o teorema de pitágoras.
, é o teorema de pitágoras. .
.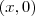 e no eixo Y da forma
e no eixo Y da forma 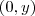 .
.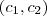 a equação da circunferência com este centro e raio
a equação da circunferência com este centro e raio  será
será 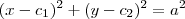 . Dados os pontos, sabemos que
. Dados os pontos, sabemos que 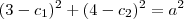 e
e 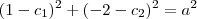 . Temos duas equações com três incógnitas, isso mostra que existem várias circunferências com diferentes raios passando por esses dois pontos.
. Temos duas equações com três incógnitas, isso mostra que existem várias circunferências com diferentes raios passando por esses dois pontos.![\sqrt{[(x+2) - 3]^2 + [-3 - (x-3)]^2} = 5 \sqrt{[(x+2) - 3]^2 + [-3 - (x-3)]^2} = 5](/latexrender/pictures/04ce04db0737b15197eba4f17cc8600f.png)
![\left[\sqrt{(x- 1)^2 + (-x)^2}\right]^2 = 5^2 \left[\sqrt{(x- 1)^2 + (-x)^2}\right]^2 = 5^2](/latexrender/pictures/9e389387fbd1a02b98b39eac037e901b.png)
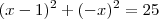
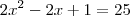
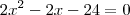
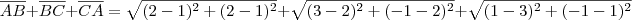
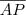 e
e 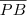 possuem a mesma medida, já que A e B são equidistantes de P.
possuem a mesma medida, já que A e B são equidistantes de P.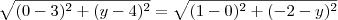
![\left[\sqrt{9 + (y-4)^2}\right]^2 = \left[\sqrt{1 + (-2-y)^2}\right]^2 \left[\sqrt{9 + (y-4)^2}\right]^2 = \left[\sqrt{1 + (-2-y)^2}\right]^2](/latexrender/pictures/b1e48bcc4bf3402bbe08aa4e5a325e97.png)

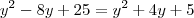
 .
.![\sqrt{(x-1)^2 + (-x-4)^2} = \sqrt{(2-x)^2 + [-5-(-x)]^2} \sqrt{(x-1)^2 + (-x-4)^2} = \sqrt{(2-x)^2 + [-5-(-x)]^2}](/latexrender/pictures/2ed36113a54fa2395866f4572ffeb7e9.png)
![\left[\sqrt{(x-1)^2 + (-x-4)^2}\right]^2 = \left[\sqrt{(2-x)^2 + (-5+x)^2}\right]^2 \left[\sqrt{(x-1)^2 + (-x-4)^2}\right]^2 = \left[\sqrt{(2-x)^2 + (-5+x)^2}\right]^2](/latexrender/pictures/f686b9294d60060cee02cf5a0efc7373.png)

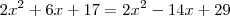
 . Usando essa informação, fica fácil concluir o exercício.
. Usando essa informação, fica fácil concluir o exercício. .
.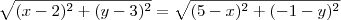
![\left[\sqrt{(x-2)^2 + (y-3)^2}\right]^2 = \left[\sqrt{(5-x)^2 + (-1-y)^2}\right]^2 \left[\sqrt{(x-2)^2 + (y-3)^2}\right]^2 = \left[\sqrt{(5-x)^2 + (-1-y)^2}\right]^2](/latexrender/pictures/7491e548d11b7a23d1af6c23fa50bb65.png)
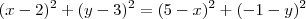

 (já que a distância do centro de uma circunferência até qualquer um de seus pontos é sempre igual. Além disso, chamamos essa distância de raio.).
(já que a distância do centro de uma circunferência até qualquer um de seus pontos é sempre igual. Além disso, chamamos essa distância de raio.).![\sqrt{(x-3)^2 + (y-4)^2} = \sqrt{(x-1)^2 + [y-(-2)]^2} \sqrt{(x-3)^2 + (y-4)^2} = \sqrt{(x-1)^2 + [y-(-2)]^2}](/latexrender/pictures/a9bfd1308a51a0f1eb3b6236dae8b3db.png)
![\left[\sqrt{(x-3)^2 + (y-4)^2}\right]^2 = \left[\sqrt{(x-1)^2 + (y+2)^2}\right]^2 \left[\sqrt{(x-3)^2 + (y-4)^2}\right]^2 = \left[\sqrt{(x-1)^2 + (y+2)^2}\right]^2](/latexrender/pictures/3b03d45d94ea556b3a14904069fc9587.png)

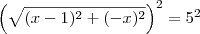
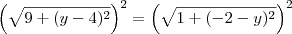
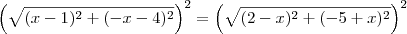
 .
. ,
,  e para
e para  ,
,  .
.
 , monte a função e substitua
, monte a função e substitua  por
por  .
.
