Não consegui resolver o seguinte sistema
obs: Pelo método de Gauss Jordan
2x + y - 2z = 10
3x + 2y + 2z = 1
5x + 4y + 3z = 4



Claudin escreveu:Não consegui resolver o seguinte sistema
obs: Pelo método de Gauss Jordan
2x + y - 2z = 10
3x + 2y + 2z = 1
5x + 4y + 3z = 4
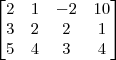
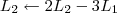
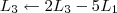
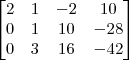
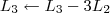
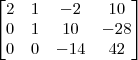
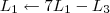
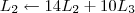
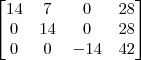
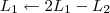
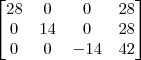
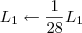
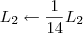
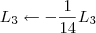
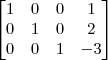


Claudin escreveu:Esse método pelo qual você explicou não seria o escalonamento?
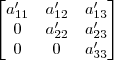
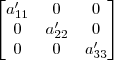
Claudin escreveu:O método de Gauss Jordan que aprendi seria transformar em "pivôs", no caso a¹¹, a²² e o a³³, no caso esses 3 valores sendo igual a 1.
Aí sim, efetuar as operações elementares, para zerar as colunas e linhas.


Voltar para Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.