 por mdiego » Ter Fev 07, 2012 22:07
por mdiego » Ter Fev 07, 2012 22:07
Descobrir os valores de
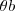
e
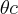
que satisfazem as seguintes equações:
Vb

Sen(
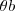
) +
![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png)
Vb

cos(
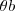
) + Vc

Sen(
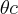
) -
![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png)
Vc

cos(
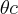
) = 0
Vb

cos(
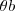
) -
![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png)
Vb

Sen(
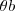
) + Vc

cos(
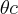
) +
![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png)
Vc

Sen(
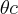
) + 1= 0
Os valores de Vb e Vc são conhecidos, e os ângulos
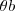
e
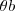
é menor do que 360º.
Não sei se há algum método matemático para resolver esse sistema. É um problema de engenharia, devo entrar com valores de Vb e Vc no Matlab e obter os respectivos ângulos. Provavelmente deve haver mais de uma solução possível.
-
mdiego
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Fev 07, 2012 21:38
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por LuizAquino » Ter Fev 07, 2012 23:49
por LuizAquino » Ter Fev 07, 2012 23:49
mdiego escreveu:Descobrir os valores de
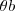
e
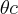
que satisfazem as seguintes equações:
![Vb\cdotSen(\theta b) + \sqrt[]{3}Vb\cdotcos(\theta b) + Vc\cdotSen(\theta c) - \sqrt[]{3}Vc\cdotcos(\theta c) = 0 Vb\cdotSen(\theta b) + \sqrt[]{3}Vb\cdotcos(\theta b) + Vc\cdotSen(\theta c) - \sqrt[]{3}Vc\cdotcos(\theta c) = 0](/latexrender/pictures/14f1b2788954ba964503050ff2995bfc.png)
![Vb\cdotcos(\theta b) - \sqrt[]{3}Vb\cdotSen(\theta b) + Vc\cdotcos(\theta c) + \sqrt[]{3}Vc\cdotSen(\theta c) + 1= 0 Vb\cdotcos(\theta b) - \sqrt[]{3}Vb\cdotSen(\theta b) + Vc\cdotcos(\theta c) + \sqrt[]{3}Vc\cdotSen(\theta c) + 1= 0](/latexrender/pictures/98d534ec77fe0e515172c559f433b4f7.png)
Os valores de Vb e Vc são conhecidos, e os ângulos
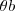
e
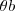
é menor do que 360º.
mdiego escreveu:Não sei se há algum método matemático para resolver esse sistema.
Utilize um método de resolução para sistemas não lineares. Por exemplo, vide os métodos descritos nessa página:
Métodos Iterativos - Sistemas Não Lineareshttp://www.math.ist.utl.pt/~calves/cour ... pii23.htmlmdiego escreveu:É um problema de engenharia, devo entrar com valores de Vb e Vc no Matlab e obter os respectivos ângulos.
Consulte a página de ajuda do programa:
Solve system of nonlinear equations - MATLABhttp://www.mathworks.com/help/toolbox/o ... solve.html
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por mdiego » Qua Fev 08, 2012 13:52
por mdiego » Qua Fev 08, 2012 13:52
Valeu pela dica Luiz!
Pelo visto terei mesmo que recorrer a esse método. Estou vendo ainda se realmente será necessário resolver o sistema, mas se for preciso já sei como solucioná-lo.
-
mdiego
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Fev 07, 2012 21:38
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [sistema linear homogeneo] Como resolver esse sistema
por amigao » Qua Jul 02, 2014 14:49
- 1 Respostas
- 3093 Exibições
- Última mensagem por Russman

Qua Jul 02, 2014 18:38
Álgebra Linear
-
- [Sistema linear] Sistema linear com constante
por smlspirit » Qui Jul 19, 2012 19:34
- 4 Respostas
- 5568 Exibições
- Última mensagem por Russman

Qui Jul 19, 2012 22:40
Sistemas de Equações
-
- [Sistema Linear] MACK-SP: Sistema de Equações
por ALF » Sex Ago 26, 2011 13:24
- 1 Respostas
- 4502 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 12:57
Sistemas de Equações
-
- Sistema linear
por kael » Ter Out 20, 2009 14:14
- 1 Respostas
- 2679 Exibições
- Última mensagem por kael

Ter Out 20, 2009 16:24
Sistemas de Equações
-
- Sistema Linear
por kael » Qua Out 21, 2009 13:43
- 1 Respostas
- 3642 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2009 15:26
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
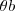 e
e 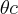 que satisfazem as seguintes equações:
que satisfazem as seguintes equações: Sen(
Sen(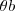 ) +
) + ![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png) Vb
Vb cos(
cos(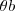 ) + Vc
) + Vc Sen(
Sen(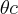 ) -
) - ![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png) Vc
Vc cos(
cos(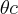 ) = 0
) = 0 cos(
cos(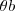 ) -
) - ![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png) Vb
Vb Sen(
Sen(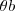 ) + Vc
) + Vc cos(
cos(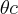 ) +
) + ![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png) Vc
Vc Sen(
Sen(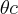 ) + 1= 0
) + 1= 0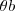 e
e 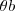 é menor do que 360º.
é menor do que 360º.

![Vb\cdotSen(\theta b) + \sqrt[]{3}Vb\cdotcos(\theta b) + Vc\cdotSen(\theta c) - \sqrt[]{3}Vc\cdotcos(\theta c) = 0 Vb\cdotSen(\theta b) + \sqrt[]{3}Vb\cdotcos(\theta b) + Vc\cdotSen(\theta c) - \sqrt[]{3}Vc\cdotcos(\theta c) = 0](/latexrender/pictures/14f1b2788954ba964503050ff2995bfc.png)
![Vb\cdotcos(\theta b) - \sqrt[]{3}Vb\cdotSen(\theta b) + Vc\cdotcos(\theta c) + \sqrt[]{3}Vc\cdotSen(\theta c) + 1= 0 Vb\cdotcos(\theta b) - \sqrt[]{3}Vb\cdotSen(\theta b) + Vc\cdotcos(\theta c) + \sqrt[]{3}Vc\cdotSen(\theta c) + 1= 0](/latexrender/pictures/98d534ec77fe0e515172c559f433b4f7.png)

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.