 por Joaozulu » Sáb Fev 04, 2012 17:22
por Joaozulu » Sáb Fev 04, 2012 17:22
(16:55:22) Joaozulu: Não consigo concluir a seguinte questão: 27!=n.10^p.
(16:57:17) Joaozulu: Minha tentativa: 27.26!=n.10^p => 26!=10^p => log 26!=p ... Faz sentido?
-
Joaozulu
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Fev 04, 2012 16:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Direito
- Andamento: formado
 por Arkanus Darondra » Sáb Fev 04, 2012 18:09
por Arkanus Darondra » Sáb Fev 04, 2012 18:09
A questão possui enunciado? Se sim, coloque-o.
Somente assim poderemos ver se faz sentido o que você fez.
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Joaozulu » Seg Fev 06, 2012 22:26
por Joaozulu » Seg Fev 06, 2012 22:26
(UNB-DF) Admita que 27!=n.10^p, em que n e p são números naturais e n não é múltiplo de 10. Calcule o valor de p.
-
Joaozulu
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Fev 04, 2012 16:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Direito
- Andamento: formado
 por LuizAquino » Ter Fev 07, 2012 14:58
por LuizAquino » Ter Fev 07, 2012 14:58
Joaozulu escreveu:(UNB-DF) Admita que 27!=n.10^p, em que n e p são números naturais e n não é múltiplo de 10. Calcule o valor de p.
Desenvolvendo a equação, temos que:
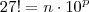
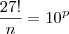
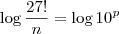
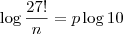
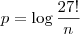
Decompondo 27! em fatores primos, temos que
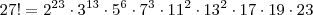
Agora podemos reescrever como:
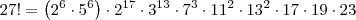
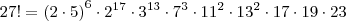
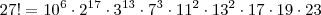
Como
p deve ser natural, o número
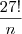
que aparece dentro do logaritmo (na base 10) deve ser uma potência de 10. Para que isso aconteça, devemos ter:
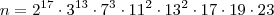
Note que sendo
n esse valor, ele não será múltiplo de dez (o que obedece ao enunciado do exercício).
Ficamos então com:
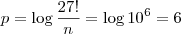
Portanto, temos que
p = 6.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- como resolver essa questao
por Thassya » Qui Mai 21, 2009 23:25
- 1 Respostas
- 4217 Exibições
- Última mensagem por marciommuniz

Sex Mai 22, 2009 12:23
Trigonometria
-
- Como resolver essa questão?
por jmoura » Sáb Mar 31, 2012 23:58
- 3 Respostas
- 2667 Exibições
- Última mensagem por NMiguel

Dom Abr 01, 2012 19:13
Cálculo: Limites, Derivadas e Integrais
-
- Como resolver essa questão da Ufpel?
 por ativirginis » Seg Fev 27, 2012 15:02
por ativirginis » Seg Fev 27, 2012 15:02
- 1 Respostas
- 5184 Exibições
- Última mensagem por LuizAquino

Ter Fev 28, 2012 18:41
Funções
-
- Sem ideia de como resolver essa questão.
por jemourafer » Sáb Abr 28, 2012 00:38
- 1 Respostas
- 1606 Exibições
- Última mensagem por Russman

Sáb Abr 28, 2012 04:52
Cálculo: Limites, Derivadas e Integrais
-
- Como resolver essa questão de probabilidade
por amanda s » Sex Nov 15, 2013 15:11
- 1 Respostas
- 2771 Exibições
- Última mensagem por DanielFerreira

Sex Nov 29, 2013 00:33
Probabilidade
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





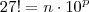
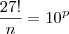
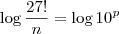
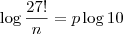
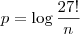
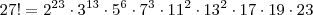
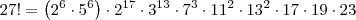
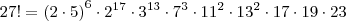
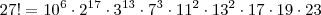
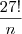 que aparece dentro do logaritmo (na base 10) deve ser uma potência de 10. Para que isso aconteça, devemos ter:
que aparece dentro do logaritmo (na base 10) deve ser uma potência de 10. Para que isso aconteça, devemos ter: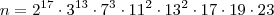
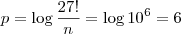

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
