Boa noite!
Gostaria de saber,como achar o Contradominio de uma função recorrendo aos Limites...sem usar o "vulgar processo" da função inversa.
Obrigado,
Abraço
Pedro Oliveira.



matpet92 escreveu:Gostaria de saber, como achar o Contradominio de uma função recorrendo aos Limites... sem usar o "vulgar processo" da função inversa.
 .
. também poderia ser tomado como contradomínio de f. Por exemplo, não haveria erro em dizer que o conjunto
também poderia ser tomado como contradomínio de f. Por exemplo, não haveria erro em dizer que o conjunto 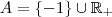 é um contradomínio para essa função f.
é um contradomínio para essa função f.

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

