 por Andrewo » Sex Jan 27, 2012 10:20
por Andrewo » Sex Jan 27, 2012 10:20
Eaaí galera, mais uma vez eu aqui com Fatoração.
Eu sei que é difícil responder e fdemorado fazer as respostas usando o editor de formulas mas eu preciso insistir nesse assunto, faz tempo que eu terminei os estudos (não lembro de mta coisa) e segundo me disseram é imprescindível que eu domine as fatorações se eu quiser avançar na matemática pq muitas coisas lá na frente vai ser necessário mta fatoração.
Então tenho 4 probleminhas aqui que deram um nó na cabeça e eu não consegui desenvolver.
1) Se 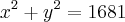 e
e  , calcule
, calcule  , sabendo que x e y são números positivos.
, sabendo que x e y são números positivos.
Resposta : 49
2)Seja a expressão 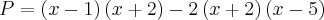
Se 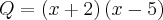
, simplifique o quociente

Resposta :
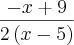
3)Simplifique a expressão
![E = {\left(\sqrt[]{28} - \sqrt[]{24} \right)}^{4} . {\left(\sqrt[]{28} + \sqrt[]{24} \right)}^{4 E = {\left(\sqrt[]{28} - \sqrt[]{24} \right)}^{4} . {\left(\sqrt[]{28} + \sqrt[]{24} \right)}^{4](/latexrender/pictures/83f876cf2318188e9fbc80c8003ac919.png)
Resposta : 64
4) Se x =
![\sqrt[]{3} + 1 \sqrt[]{3} + 1](/latexrender/pictures/ee55d11df65c893d0ddcfba13bff4395.png)
, calcule
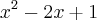
[/b]
Conto consigo

-

Andrewo
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Qui Jan 12, 2012 11:22
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por fraol » Sex Jan 27, 2012 11:39
por fraol » Sex Jan 27, 2012 11:39
Olá, vou tratar do problema número 1:
Andrewo escreveu:1) Se
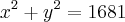
e

, calcule

, sabendo que x e y são números positivos.
Resposta : 49
Você há de se lembrar do produto notável:
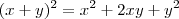
.
( quadrado do primeiro, mais duas vezes o primeiro pelo segundo + o quadrado do segundo).
Que rearranjando fica assim:
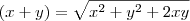
.
Agora é só substituir os valores do enunciado que a resposta vem.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Arkanus Darondra » Sex Jan 27, 2012 12:44
por Arkanus Darondra » Sex Jan 27, 2012 12:44
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Andrewo » Sex Jan 27, 2012 16:24
por Andrewo » Sex Jan 27, 2012 16:24
O problema dessas listas de exercício tiradas da internet é esse; não tem mta credibilidade, mtos erros na resposta e tal.
Mas obrigado pela ajuda, não entendi mto bem o que o fraol fez ali, ele tirou a potencia e transformou numa raiz do outro lado?Em que ocasiões podemos fazer isso?As fatorações são mesmo mto importantes pra qm tá estudando?

-

Andrewo
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Qui Jan 12, 2012 11:22
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Arkanus Darondra » Sex Jan 27, 2012 16:39
por Arkanus Darondra » Sex Jan 27, 2012 16:39
Andrewo escreveu:O problema dessas listas de exercício tiradas da internet é esse; não tem mta credibilidade, mtos erros na resposta e tal.
Mas obrigado pela ajuda, não entendi mto bem o que o fraol fez ali, ele tirou a potencia e transformou numa raiz do outro lado?Em que ocasiões podemos fazer isso?
Sim. Em qualquer equação, quaisquer operações que sejam feitas em ambos os lados, não alterará o resultado.
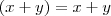

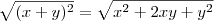
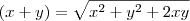

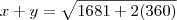
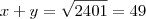
Andrewo escreveu:As fatorações são mesmo mto importantes pra qm tá estudando?
Assuntos como fatoração, radiciação, potenciação, equações do primeiro e segundo grau, regra de três, dentre outros, são essenciais.

Editado pela última vez por
Arkanus Darondra em Sex Jan 27, 2012 17:26, em um total de 1 vez.
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por ant_dii » Sex Jan 27, 2012 17:05
por ant_dii » Sex Jan 27, 2012 17:05
Você pretende fazer um curso de exatas??
Se for esse o caso, conta mais a experiência que você tem em resolver problemas de todo o tipo (o que envolve naturalmente a fatoração)... É interessante você estudar este tema mas procure ser critico vendo-o durante alguns exercícios... Para ilustrar o que falo, temos o caso em que
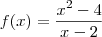
onde f é uma função, conceito que provavelmente você já estudou... Existe um conceito, pouco avançado em sentido de série, talvez, que se chama limite em que você estudará algumas propriedades dessa função. Não vou me delongar nisso, mas basicamente, digamos que seja necessário substituir x por 2, ou seja, calcular
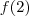
. Você não poderá pois a função retorna uma indeterminação... Neste caso, para determinar como a função se comporta próximo do ponto x=2, você deverá fazer uma simples manipulação, assim
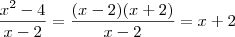
que pode ser feito x=2 e retornará 4 como resultado.
Tomara que não compliquei...
Mas não se preocupe com uma coisa (um conceito) em específico, estudar matemática é muito bom e até mesmo vicia, digamos assim. Então em nada você perderá já que você esta interessado...
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por Andrewo » Sáb Jan 28, 2012 11:27
por Andrewo » Sáb Jan 28, 2012 11:27
ant_dii escreveu:Você pretende fazer um curso de exatas??
Se for esse o caso, conta mais a experiência que você tem em resolver problemas de todo o tipo (o que envolve naturalmente a fatoração)... É interessante você estudar este tema mas procure ser critico vendo-o durante alguns exercícios... Para ilustrar o que falo, temos o caso em que
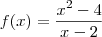
onde f é uma função, conceito que provavelmente você já estudou... Existe um conceito, pouco avançado em sentido de série, talvez, que se chama limite em que você estudará algumas propriedades dessa função. Não vou me delongar nisso, mas basicamente, digamos que seja necessário substituir x por 2, ou seja, calcular
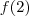
. Você não poderá pois a função retorna uma indeterminação... Neste caso, para determinar como a função se comporta próximo do ponto x=2, você deverá fazer uma simples manipulação, assim
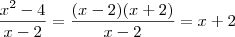
que pode ser feito x=2 e retornará 4 como resultado.
Tomara que não compliquei...
Mas não se preocupe com uma coisa (um conceito) em específico, estudar matemática é muito bom e até mesmo vicia, digamos assim. Então em nada você perderá já que você esta interessado...
Sim, vou fazer um curso de exatas,
Não complicou não, uma coisa puxa a outra, é bom dominar tudo.Graças a deus tenho revisto e aprendido mta coisa.
Comecei revisando tudo,começando pelas operações mais simples que não lembrava mais.Ainda tenho mto que aprender então conto com a ajuda aí

-

Andrewo
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Qui Jan 12, 2012 11:22
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [fatoração] fatoração de polinômio do quarto grau.
por +Danilo2 » Qui Set 29, 2016 10:43
- 5 Respostas
- 8654 Exibições
- Última mensagem por +Danilo2

Sáb Out 08, 2016 18:17
Polinômios
-
- fatoração de Polinômio fatoração de agrupamento
por Estudante13 » Sex Nov 09, 2012 22:52
- 1 Respostas
- 3121 Exibições
- Última mensagem por Cleyson007

Sex Nov 09, 2012 23:06
Álgebra Elementar
-
- [fatoração] Exercício de Fatoração
por Cleyson007 » Qua Abr 30, 2008 00:39
- 3 Respostas
- 8720 Exibições
- Última mensagem por admin

Qua Abr 30, 2008 02:15
Álgebra Elementar
-
- Fatoração
por Rogerioeetc » Sex Jul 24, 2009 02:00
- 2 Respostas
- 2458 Exibições
- Última mensagem por Rogerioeetc

Dom Jul 26, 2009 14:26
Álgebra Elementar
-
- Fatoração
por Jaqueline Pimenta » Qui Out 01, 2009 11:50
- 5 Respostas
- 3951 Exibições
- Última mensagem por Jaqueline Pimenta

Seg Out 05, 2009 12:05
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e  , calcule
, calcule  , sabendo que x e y são números positivos.
, sabendo que x e y são números positivos.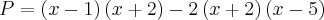
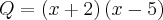 , simplifique o quociente
, simplifique o quociente 
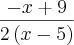
![E = {\left(\sqrt[]{28} - \sqrt[]{24} \right)}^{4} . {\left(\sqrt[]{28} + \sqrt[]{24} \right)}^{4 E = {\left(\sqrt[]{28} - \sqrt[]{24} \right)}^{4} . {\left(\sqrt[]{28} + \sqrt[]{24} \right)}^{4](/latexrender/pictures/83f876cf2318188e9fbc80c8003ac919.png)
![\sqrt[]{3} + 1 \sqrt[]{3} + 1](/latexrender/pictures/ee55d11df65c893d0ddcfba13bff4395.png) , calcule
, calcule 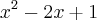



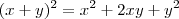 .
.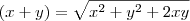 .
.
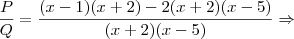
![\frac{P}{Q}=\frac{(x+2)[(x-1)-2(x-5)]}{(x+2)(x-5)} \Rightarrow \frac{P}{Q}=\frac{(x+2)[(x-1)-2(x-5)]}{(x+2)(x-5)} \Rightarrow](/latexrender/pictures/d5f8360a82c06c3668a18badd69c0fe9.png)
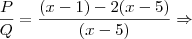
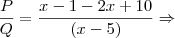
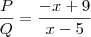
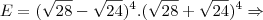
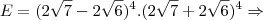
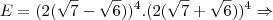
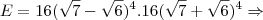
![E=256.[(\sqrt7-\sqrt6)(\sqrt7+\sqrt6)]^4 \Rightarrow E=256.[(\sqrt7-\sqrt6)(\sqrt7+\sqrt6)]^4 \Rightarrow](/latexrender/pictures/c9dfb953d065ab21e304edb0facca095.png)
![E=256.[(\sqrt7)^2-(\sqrt6)^2]^4 \Rightarrow E=256.[(\sqrt7)^2-(\sqrt6)^2]^4 \Rightarrow](/latexrender/pictures/f03510ece8213ab85afd9dfe29ea3e60.png)
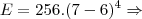
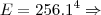


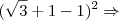
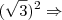

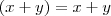

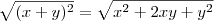
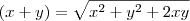

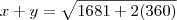
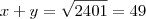
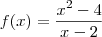
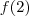 . Você não poderá pois a função retorna uma indeterminação... Neste caso, para determinar como a função se comporta próximo do ponto x=2, você deverá fazer uma simples manipulação, assim
. Você não poderá pois a função retorna uma indeterminação... Neste caso, para determinar como a função se comporta próximo do ponto x=2, você deverá fazer uma simples manipulação, assim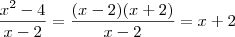
 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: