 por nathyn » Qua Jan 25, 2012 19:20
por nathyn » Qua Jan 25, 2012 19:20
Oie, sei que é meio besta a questão, mas ta ae:
![{x}^{\sqrt[2]{x}}=\sqrt[2]{{x}^{x}} {x}^{\sqrt[2]{x}}=\sqrt[2]{{x}^{x}}](/latexrender/pictures/11ed5e2d9b827ee6aecc86096da1a44c.png)
Eu tentei fazer elevando ambos os lados ao quadrado, e assim fazendo encontrei:
![{x}^{\sqrt[2]{2x}}= {x}^{x} {x}^{\sqrt[2]{2x}}= {x}^{x}](/latexrender/pictures/e7e12b00ae120c209c369b610862e79b.png)
Sei q está errado pois achei como resposta x=2, mas a resposta do livro é: 0,1 e 4
Me ajudem ae por favor... Brigada.
-
nathyn
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Qua Nov 16, 2011 14:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por ant_dii » Qua Jan 25, 2012 20:26
por ant_dii » Qua Jan 25, 2012 20:26
Olha, eu encontrei a as ráizes x=4 e x=0, mas não encontrei a raíz x=1 com manipulação algébrica...
Fiz o seguinte
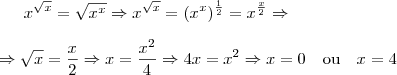
Mas a raíz x=1 é óbvia...
O problema é quando x=0. Provavelmente o seu livro esta errado, pois não há definição (pelo menos que seja trivial para o ensino médio) para

.
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por nathyn » Qui Jan 26, 2012 12:34
por nathyn » Qui Jan 26, 2012 12:34
Pooo brigadão, o livro é aquele fundamentos da matematica elementar, mas o q mais importava mesmo
era a extração da raiz que eu não tava sabendo fazer certo.
Muito obrigada ;D
-
nathyn
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Qua Nov 16, 2011 14:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação - Dúvida básica sobre a proporcionalidade de equação
por FelipeGM » Qui Jan 12, 2012 19:05
- 4 Respostas
- 7735 Exibições
- Última mensagem por FelipeGM

Sáb Jan 14, 2012 13:16
Álgebra Elementar
-
- Equação - como montar a equação desse problema?
por _Manu » Qua Jul 04, 2012 03:37
- 7 Respostas
- 13238 Exibições
- Última mensagem por _Manu

Qui Jul 05, 2012 01:49
Sistemas de Equações
-
- [Equação polinomial] Ajuda com essa equação?
por Mkdj21 » Sáb Jan 26, 2013 16:19
- 1 Respostas
- 13030 Exibições
- Última mensagem por young_jedi

Dom Jan 27, 2013 17:15
Equações
-
- [Equação da reta] Encontrando equação paramétrica.
por Vitor Sanches » Qua Jun 26, 2013 17:54
- 0 Respostas
- 6098 Exibições
- Última mensagem por Vitor Sanches

Qua Jun 26, 2013 17:54
Geometria Analítica
-
- Equação - Como resolver problema com equação
por macedo1967 » Seg Set 25, 2017 10:13
- 3 Respostas
- 8720 Exibições
- Última mensagem por DanielFerreira

Dom Out 08, 2017 20:10
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![{x}^{\sqrt[2]{x}}=\sqrt[2]{{x}^{x}} {x}^{\sqrt[2]{x}}=\sqrt[2]{{x}^{x}}](/latexrender/pictures/11ed5e2d9b827ee6aecc86096da1a44c.png)
![{x}^{\sqrt[2]{2x}}= {x}^{x} {x}^{\sqrt[2]{2x}}= {x}^{x}](/latexrender/pictures/e7e12b00ae120c209c369b610862e79b.png)

![{x}^{\sqrt[2]{x}}=\sqrt[2]{{x}^{x}} {x}^{\sqrt[2]{x}}=\sqrt[2]{{x}^{x}}](/latexrender/pictures/11ed5e2d9b827ee6aecc86096da1a44c.png)
![{x}^{\sqrt[2]{2x}}= {x}^{x} {x}^{\sqrt[2]{2x}}= {x}^{x}](/latexrender/pictures/e7e12b00ae120c209c369b610862e79b.png)

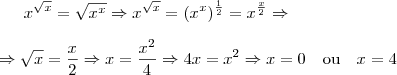
 .
.

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
