 por Cleyson007 » Qua Out 29, 2008 00:28
por Cleyson007 » Qua Out 29, 2008 00:28
Olá, boa noite!!!
Alguém pode me ajudar na resolução do seguinte exercício?
Estou completamente perdido

Seja
![f: D \rightarrow\Re, com [tex]D\subset\Re f: D \rightarrow\Re, com [tex]D\subset\Re](/latexrender/pictures/4a93fe829278f2a8d0dfc0f7caf93704.png)
, a função definida por
![f(x)= \sqrt[2]{5-x}+\frac{1}{\sqrt[2]{x+1}} f(x)= \sqrt[2]{5-x}+\frac{1}{\sqrt[2]{x+1}}](/latexrender/pictures/f5dea3d4686d365063dc6986eb8c1ab1.png)
. O domínio
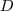
da função pode ser descrito como:
a) [-1,5]
b) [5,

]
c) ]5,

[
d) ]-1,5]
e) ]5,

[- {-1}
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por admin » Qua Out 29, 2008 02:02
por admin » Qua Out 29, 2008 02:02
Olá Cleyson, boa noite!
Nestes casos o domínio pertencente aos Reais fica determinado resolvendo "os problemas" que a função "enfrenta".
Exemplos de "problemas": o denominador não pode ser zero; o radicando não pode ser negativo.
Combine estas possibilidades impondo restrições ao

através de inequações.
Assim, encontrando um conjunto que atenda às condições impostas, ele será o domínio da função.
Bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Cleyson007 » Seg Jun 01, 2009 12:38
por Cleyson007 » Seg Jun 01, 2009 12:38
fabiosousa escreveu:Olá Cleyson, boa noite!
Nestes casos o domínio pertencente aos Reais fica determinado resolvendo "os problemas" que a função "enfrenta".
Exemplos de "problemas": o denominador não pode ser zero; o radicando não pode ser negativo.
Combine estas possibilidades impondo restrições ao

através de inequações.
Assim, encontrando um conjunto que atenda às condições impostas, ele será o domínio da função.
Bons estudos!
Bom dia Fabio Sousa!
Estou revendo alguns tópicos que ficaram "pendentes".
Quanto a citação acima: O denominador (
![\sqrt[2]{x+1} \sqrt[2]{x+1}](/latexrender/pictures/1a4918c18d7e32bcc010b0b56b47de5f.png)
)
Logo,
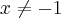
Quanto ao numerador,

deve ser
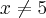

também deve ser
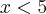
Como prosseguir?
Agradeço sua ajuda!
Um abraço.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Funções] Domínio e a imagem de funções
 por concurseironf » Qui Ago 21, 2014 12:24
por concurseironf » Qui Ago 21, 2014 12:24
- 1 Respostas
- 4199 Exibições
- Última mensagem por Pessoa Estranha

Sex Ago 22, 2014 20:11
Funções
-
- Domínio das funções
 por kellykcl » Qui Abr 10, 2014 20:18
por kellykcl » Qui Abr 10, 2014 20:18
- 2 Respostas
- 2158 Exibições
- Última mensagem por kellykcl

Sex Abr 11, 2014 14:15
Funções
-
- Funções - Intervalo, Domínio
por jorgeltpereira » Seg Dez 08, 2008 10:33
- 1 Respostas
- 1776 Exibições
- Última mensagem por Neperiano

Qua Ago 24, 2011 15:07
Funções
-
- Funções:Domínio e Imagem
por +Julia » Sáb Abr 12, 2014 09:54
- 0 Respostas
- 1149 Exibições
- Última mensagem por +Julia

Sáb Abr 12, 2014 09:54
Funções
-
- Dominio de funções, ajuda por favor ?
por fabio155nike » Qui Jul 17, 2014 15:58
- 0 Respostas
- 1382 Exibições
- Última mensagem por fabio155nike

Qui Jul 17, 2014 15:58
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

![f: D \rightarrow\Re, com [tex]D\subset\Re f: D \rightarrow\Re, com [tex]D\subset\Re](/latexrender/pictures/4a93fe829278f2a8d0dfc0f7caf93704.png) , a função definida por
, a função definida por ![f(x)= \sqrt[2]{5-x}+\frac{1}{\sqrt[2]{x+1}} f(x)= \sqrt[2]{5-x}+\frac{1}{\sqrt[2]{x+1}}](/latexrender/pictures/f5dea3d4686d365063dc6986eb8c1ab1.png) . O domínio
. O domínio 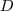 da função pode ser descrito como:
da função pode ser descrito como:  ]
] [
[ [- {-1}
[- {-1}

![f: D \rightarrow\Re, com [tex]D\subset\Re f: D \rightarrow\Re, com [tex]D\subset\Re](/latexrender/pictures/4a93fe829278f2a8d0dfc0f7caf93704.png) , a função definida por
, a função definida por ![f(x)= \sqrt[2]{5-x}+\frac{1}{\sqrt[2]{x+1}} f(x)= \sqrt[2]{5-x}+\frac{1}{\sqrt[2]{x+1}}](/latexrender/pictures/f5dea3d4686d365063dc6986eb8c1ab1.png) . O domínio
. O domínio 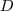 da função pode ser descrito como:
da função pode ser descrito como:  ]
] [
[ [- {-1}
[- {-1}
 através de inequações.
através de inequações.
através de inequações.
![\sqrt[2]{x+1} \sqrt[2]{x+1}](/latexrender/pictures/1a4918c18d7e32bcc010b0b56b47de5f.png) )
)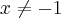
 deve ser
deve ser 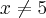
 também deve ser
também deve ser 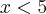



 , avisa que eu resolvo.
, avisa que eu resolvo.

