 por lourivallobo » Ter Jan 24, 2012 20:49
por lourivallobo » Ter Jan 24, 2012 20:49
Para montar a senha de segurança de sua conta bancá-
ria, que deve ser formada por seis dígitos, João escolheu
1, 2, 5, 5, 7 e 8. Os dígitos escolhidos não serão dispostos
na ordem apresentada, pois, para João, é importante que
a senha seja um número maior do que 500.000.
Com os dígitos escolhidos por João, quantas senhas
maiores do que 500.000 podem ser formadas?
(A) 720
(B) 600
(C) 360
(D) 240
(E) 120
-
lourivallobo
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Jan 24, 2012 20:38
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Telecomunicações
- Andamento: formado
 por LuizAquino » Ter Jan 24, 2012 21:51
por LuizAquino » Ter Jan 24, 2012 21:51
lourivallobo escreveu:Para montar a senha de segurança de sua conta bancá-
ria, que deve ser formada por seis dígitos, João escolheu
1, 2, 5, 5, 7 e 8. Os dígitos escolhidos não serão dispostos
na ordem apresentada, pois, para João, é importante que
a senha seja um número maior do que 500.000.
Com os dígitos escolhidos por João, quantas senhas
maiores do que 500.000 podem ser formadas?
(A) 720
(B) 600
(C) 360
(D) 240
(E) 120
Primeiro contabilize as senhas que começam com o dígito 5. Nesse caso, teremos:
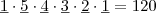
Depois considere as senhas que não começam com o dígito 5. Nesse caso, teremos:
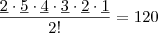
Note que nesse caso nós precisamos dividir por 2!, pois o dígito 5 é repetido duas vezes.
Sendo assim, no total temos 120 + 120 = 240 senhas possíveis.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Concurso Petrobras
 por lourivallobo » Ter Jan 24, 2012 20:47
por lourivallobo » Ter Jan 24, 2012 20:47
- 1 Respostas
- 3963 Exibições
- Última mensagem por LuizAquino

Ter Jan 24, 2012 21:12
Logaritmos
-
- Concurso Petrobras
por lourivallobo » Ter Jan 24, 2012 20:52
- 1 Respostas
- 3018 Exibições
- Última mensagem por LuizAquino

Ter Jan 24, 2012 22:08
Estatística
-
- Concurso Petrobras
 por lourivallobo » Qua Jan 25, 2012 09:13
por lourivallobo » Qua Jan 25, 2012 09:13
- 4 Respostas
- 2992 Exibições
- Última mensagem por Arkanus Darondra

Qua Jan 25, 2012 17:30
Matrizes e Determinantes
-
- PA concurso petrobras
por thiagodr » Sex Mar 23, 2012 01:07
- 3 Respostas
- 2014 Exibições
- Última mensagem por thiagodr

Sáb Abr 07, 2012 16:34
Progressões
-
- DERIVADA - CONCURSO PETROBRAS
por pinkfluor » Qua Mar 02, 2011 11:10
- 2 Respostas
- 2328 Exibições
- Última mensagem por LuizAquino

Qua Mar 02, 2011 12:06
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


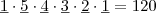
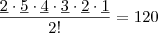

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
