 por Andreza » Ter Jan 24, 2012 10:44
por Andreza » Ter Jan 24, 2012 10:44
Em um armário há 5 pares de sapatos. Retira-se desse armário ao acaso 4 pés de sapatos. Qual a probabilidade de se formar exatamente um par de sapatos?
Eu pensei em 5x2=10 pés de sapatos
Portanto seria

Está correto?
Desde já agradeço.
-
Andreza
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Sáb Out 22, 2011 11:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenc. Plena Matemática
- Andamento: formado
 por ant_dii » Ter Jan 24, 2012 12:18
por ant_dii » Ter Jan 24, 2012 12:18
Estou tentando resolver aqui, mas acho que você deve desconfiar do seu resultado... 0,4 é uma probabilidade muito alta só para quatro pés de sapato entre 5 pares...
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por ant_dii » Ter Jan 24, 2012 12:48
por ant_dii » Ter Jan 24, 2012 12:48
Vamos tentar juntos... Probabilidade não é meu forte, mas o que sei acho que pode ajudar...
A probabilidade de se tomar 4 pés entre 10 pés é 4/10.
A probabilidade de, entre esses quatro, termos 1 par é 3/4, pois fixa-se 1 pé e teremos 3 possibilidades para combinar com ele...
Então a probabilidade é
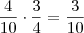
É o que eu acho... É o mais coerente que encontrei... Corrijam se possível
Veja se vc concorda, Andreza, e me fale...
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por Andreza » Ter Jan 24, 2012 13:08
por Andreza » Ter Jan 24, 2012 13:08
Sinceramente eu estou em dúvida, não tem gabarito, vou ter q estudar mais o assunto pra ver, agradeço muito a sua atenção.
-
Andreza
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Sáb Out 22, 2011 11:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenc. Plena Matemática
- Andamento: formado
 por ant_dii » Ter Jan 24, 2012 13:23
por ant_dii » Ter Jan 24, 2012 13:23
Agora, repensando a questão, percebi uma coisa. Você quer tomar 4 pés entre 10, então na verdade teríamos combinatória de 10 tomado 4 a 4, que é 210 possibilidades...
Logo , na verdade você teria
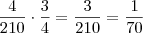
Mas faça isso mesmo que você falou, estuda o assunto e poste aqui pra sumir a dúvida.
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Pares ordenados !
por LuizCarlos » Sáb Ago 20, 2011 17:35
- 6 Respostas
- 2870 Exibições
- Última mensagem por LuizCarlos

Sáb Ago 20, 2011 23:20
Álgebra Elementar
-
- Números Pares
por Andreza » Seg Jan 23, 2012 15:38
- 2 Respostas
- 1872 Exibições
- Última mensagem por Andreza

Seg Jan 23, 2012 17:12
Estatística
-
- Funções ímpares e pares
por Zkz » Seg Set 29, 2008 23:02
- 2 Respostas
- 9036 Exibições
- Última mensagem por Molina

Ter Set 30, 2008 00:20
Funções
-
- achar o n° de divisores pares
por Valmel » Dom Jul 28, 2013 12:11
- 1 Respostas
- 4671 Exibições
- Última mensagem por young_jedi

Qua Jul 31, 2013 00:20
Álgebra Elementar
-
- Função [ pares ordenados ]
por my2009 » Qua Mai 27, 2015 18:03
- 0 Respostas
- 1327 Exibições
- Última mensagem por my2009

Qua Mai 27, 2015 18:03
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





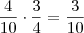


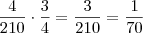



 , avisa que eu resolvo.
, avisa que eu resolvo.

