 por Thays » Sáb Jan 14, 2012 11:42
por Thays » Sáb Jan 14, 2012 11:42
Eu preciso de uma explicação para esta questão aqui:
Simplificando a expressão (a + b )² - 2ab vamos obter:
a-( ) a²+b² - 2ab
b-( ) a²+ b² - ab
c-( ) a²+ b²
d-( )a²-b²
Eu queria que vocês resolvessem ela pra mim me explicano passo a passo!
Desde já agradeço!
-
Thays
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Sáb Jan 14, 2012 11:26
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso tecnico em Farmacia
- Andamento: cursando
 por Renato_RJ » Sáb Jan 14, 2012 12:09
por Renato_RJ » Sáb Jan 14, 2012 12:09
Bom dia Thays !!
Seguinte, primeiro desenvolva o binômio
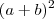
e resolva a equação, veja:
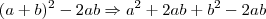
Repare que temos
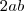
e
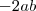
, então:
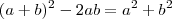
Qualquer dúvida, pode postar..
Abraços,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- SIMPLIFICANDO A EXPRESSÃO
por Jhordan Gabriel » Dom Dez 04, 2011 10:29
- 2 Respostas
- 2131 Exibições
- Última mensagem por Jhordan Gabriel

Dom Dez 04, 2011 11:01
Sistemas de Equações
-
- Simplificando expressão
por Robinho » Sáb Jan 14, 2012 12:35
- 5 Respostas
- 2178 Exibições
- Última mensagem por MarceloFantini

Sáb Jan 14, 2012 14:07
Sistemas de Equações
-
- Simplificando expressão
por Yasmin Felix » Seg Jan 16, 2012 10:58
- 1 Respostas
- 978 Exibições
- Última mensagem por ant_dii

Seg Jan 16, 2012 14:50
Funções
-
- Simplificando expressão
por Thays » Seg Jan 16, 2012 11:18
- 3 Respostas
- 1435 Exibições
- Última mensagem por Arkanus Darondra

Seg Jan 16, 2012 13:19
Sistemas de Equações
-
- Resultado para isso.. Simplificando..
por aninhawell » Dom Jun 24, 2012 12:32
- 1 Respostas
- 1086 Exibições
- Última mensagem por MarceloFantini

Seg Jun 25, 2012 01:20
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


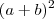 e resolva a equação, veja:
e resolva a equação, veja: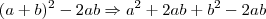
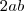 e
e 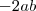 , então:
, então: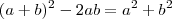

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.