A notação é:
 , em que
, em que 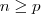 .
.Depois existe o que se chama de arranjo composto (com repetição).
A notação é:
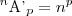
Mas julgo que nem sempre o n e o p são o mesmos em ambos os casos.
Exemplo #1:
Quantos números de 3 algarismos se podem formar com os digitos 0 e 1?
Aqui aplica-se um arranjo composto, em que n=2 e p=3.
Exemplo #2:
Numa competição participam 3 jogadores.Só existe prémio para o 1º e 2º lugares. De quantas formas diferentes se podem distribuir os prémios?
Aqui aplica-se um arranjo simples, em que n=3 e p=2.
Porque isto acontece?


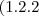 e não
e não 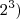 .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)