Já agora Renato precisava se conseguisses a resolução de :
Calcule a derivada total de f(x,y)=x^2+4y^2
Quando
x(t)=sin(alfat), y(t)= €cos(alfat)
onde alfa,€, são números reais positivos.
Diaga ainda se existe algum valor de € para o qual a derivada total se anula para todo o t. Se existir, calcule esse valor (ou um deles, se não for único).


 para k, então o exercício ficará assim (sem alteração no resultado final, é só uma mudança de nome):
para k, então o exercício ficará assim (sem alteração no resultado final, é só uma mudança de nome):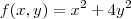
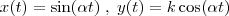
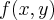 , vou considerar que você deseje derivar a função f em relação a variável t, então temos o caso seguinte:
, vou considerar que você deseje derivar a função f em relação a variável t, então temos o caso seguinte: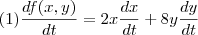
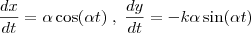
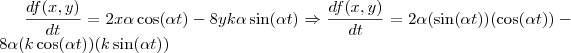
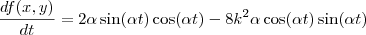
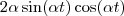 em evidência, temos:
em evidência, temos: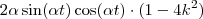
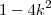 a zero, achemos as raízes dessa equação:
a zero, achemos as raízes dessa equação: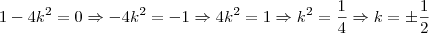



 , avisa que eu resolvo.
, avisa que eu resolvo.

