a)
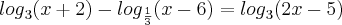
b)
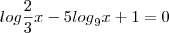
c)

As respostas são:
a)S={7}
b)S={
![{9,\sqrt[]{2}} {9,\sqrt[]{2}}](/latexrender/pictures/847bedae4d9cf81f64ffd7ddf021aa7d.png) }
}c)S={
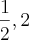 }
}Agradeço muito quem resolver esse calculo!

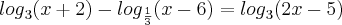
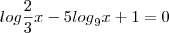

![{9,\sqrt[]{2}} {9,\sqrt[]{2}}](/latexrender/pictures/847bedae4d9cf81f64ffd7ddf021aa7d.png) }
}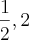 }
}
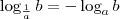 e também
e também 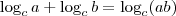 , lembrando das condições de existência.
, lembrando das condições de existência.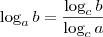 .
.

andersontricordiano escreveu:Resolva, em R, as seguintes equações:
a)
As respostas são:
a)S={7}
Agradeço muito quem resolver esse calculo!
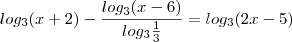
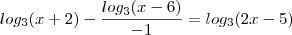
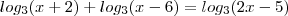
![log_{3} [(x + 2)(x - 6)] = log_{3} (2x - 5) log_{3} [(x + 2)(x - 6)] = log_{3} (2x - 5)](/latexrender/pictures/06e5ff14bd76efe4c3b96b93be199bbd.png)
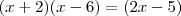
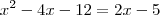
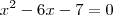
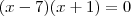
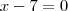


andersontricordiano escreveu:Resolva, em R, as seguintes equações:
c)
As respostas são:
c)S={}
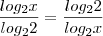
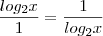
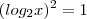
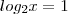 e
e 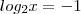
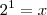 e
e 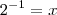
 e
e 

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)