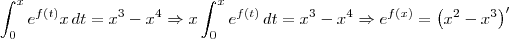por nuno » Sex Jan 06, 2012 20:06
por nuno » Sex Jan 06, 2012 20:06
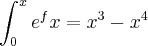
gostava que dessem informação de como resolver este tipo de derivadas
-
nuno
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Jan 06, 2012 19:34
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: licenciatura em engenharia
- Andamento: cursando
 por LuizAquino » Dom Jan 08, 2012 11:57
por LuizAquino » Dom Jan 08, 2012 11:57
nuno escreveu: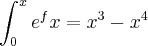
gostava que dessem informação de como resolver este tipo de derivadas
Eu presumo que no enunciado original do exercício temos algo do tipo:
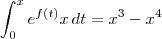
Pelo Teorema Fundamental do Cálculo (parte 1), temos que:
Se
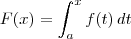
com
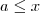
, então temos que
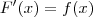
.
Desse modo, podemos escrever que:
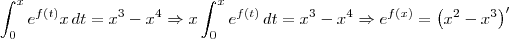
Agora tente terminar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- resolução derivada integral
por MARCIOESTUDIOSO » Seg Fev 14, 2011 10:33
- 4 Respostas
- 4102 Exibições
- Última mensagem por LuizAquino

Ter Fev 15, 2011 14:37
Cálculo: Limites, Derivadas e Integrais
-
- Encontrar a derivada de um integral
por Elvis » Seg Ago 17, 2015 13:43
- 5 Respostas
- 5499 Exibições
- Última mensagem por Elvis

Sex Ago 21, 2015 15:07
Cálculo: Limites, Derivadas e Integrais
-
- [Integral definida] calcular sua derivada
por Ge_dutra » Dom Mai 12, 2013 21:49
- 0 Respostas
- 1048 Exibições
- Última mensagem por Ge_dutra

Dom Mai 12, 2013 21:49
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo Diferencial e Integral I] Derivada
por Pessoa Estranha » Qui Set 25, 2014 13:03
- 2 Respostas
- 3457 Exibições
- Última mensagem por Pessoa Estranha

Sex Set 26, 2014 10:47
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integração e anti-derivada
por bencz » Sex Mar 18, 2016 10:42
- 1 Respostas
- 4078 Exibições
- Última mensagem por anselmojr97

Dom Mar 20, 2016 17:09
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
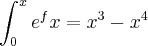 gostava que dessem informação de como resolver este tipo de derivadas
gostava que dessem informação de como resolver este tipo de derivadas

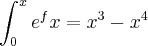 gostava que dessem informação de como resolver este tipo de derivadas
gostava que dessem informação de como resolver este tipo de derivadas
gostava que dessem informação de como resolver este tipo de derivadas
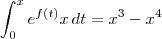
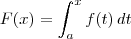 com
com 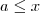 , então temos que
, então temos que 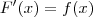 .
.