Analisando o seguinte problema:
Um exame possui 10 questões de múltipla escolha com 3 alternativas por questão. Qual é o número de gabaritos possíveis em que a primeira e a segunda alternativa aparecem, cada uma, em exatamente 3 questões?
Desenvolvi da seguinte maneira:
Sejam A, B e C as alternativas.
Para a alternativa A devemos escolher 3 questões em 10, isto é:
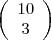 opções de gabarito.
opções de gabarito.Para a alternativa B devemos escolher 3 questões em 7 restantes, isto é:
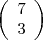 opções de gabarito.
opções de gabarito.(*) Por fim restam 4 questões para as quais a única opção é a alternativa C e portanto temos:
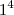 opções de gabarito.
opções de gabarito.Portanto a resposta seria:
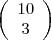
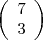
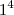 .
.Como já faz algumas décadas que não vejo o assunto, fiquei inseguro em relação ao caso (*) acima.
Concordam com o desenvolvimento que fiz?



 .
.



