Boa noite, tudo em paz ???
Seguinte, podemos representar essa promoção matematicamente da seguinte forma (veja que o problema diz "compre x balas e ganhe x% de desconto"):
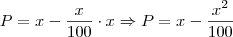
Logo a quantia a ser paga pelas balas será
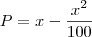
, mas o problema pede para descobrirmos como comprar mais balas gastando menos, logo temos um problema de máximo, como temos uma função de segundo grau com coeficiente líder negativo (o valor que multiplica o x de maior grau), logo o vértice da parábola descrita pela função achada representa o máximo da função, logo:
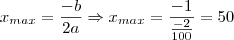
Logo, a quantidade que tem o maior desconto é de 50 balas. Agora, repare que Daniel poderia ter comprado 55 balas pelo mesmo preço que pagou pelas 45, veja:
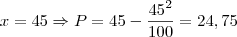
Agora vejamos com
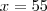
:
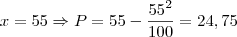
Então a resposta desejada é Daniel, pois ele poderia ter comprado 55 balas (10 balas a mais do que realmente comprou) pelo mesmo preço.
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...


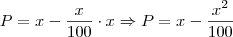
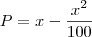 , mas o problema pede para descobrirmos como comprar mais balas gastando menos, logo temos um problema de máximo, como temos uma função de segundo grau com coeficiente líder negativo (o valor que multiplica o x de maior grau), logo o vértice da parábola descrita pela função achada representa o máximo da função, logo:
, mas o problema pede para descobrirmos como comprar mais balas gastando menos, logo temos um problema de máximo, como temos uma função de segundo grau com coeficiente líder negativo (o valor que multiplica o x de maior grau), logo o vértice da parábola descrita pela função achada representa o máximo da função, logo: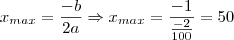
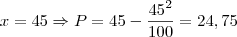
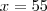 :
: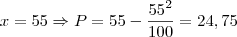

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)