Em relação a este exame, não consegui encontrar uma proposta de resolução.Por isso decidi postar aqui as questões resolvidas por mim, para que alguém possa verificar se estão bem resolvidas.
Esta questão é uma aplicação da definição de limite segundo Heine.
Obeservando a função f verificamos que o 2 é o ponto critico. Por isso

Calculando os limites laterais quando
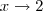 concluimos que
concluimos que  .
.Assim
 quando
quando 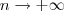
A resposta é a B.
Aqui trata-se de calcular a I derivada de g no ponto x=1 para depois encontrar a equação da reta tangente.


Agora resta encontrar g'(1)

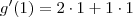

Concluimos daqui que o declive da reta tangente de g no ponto x=1 é 3. Agora falta a ordenada na origem.
Pelo enunciado sabemos a expressão analitica de g, então
 . Porque
. Porque 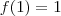 .
.Assim
 .
. Agora temos par ordenado (1,1) que basta substituir em y=3x+b e resolver em ordem a b.
A resposta é a A.
Este exame tem mais questões de funções, probabilidades e complexos.Em anexo esta o exame completo

