 por joaofonseca » Qua Nov 30, 2011 22:29
por joaofonseca » Qua Nov 30, 2011 22:29
Dada a seguinte expressão:
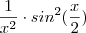
Encontre a formula da derivada.
Eu fiz assim:
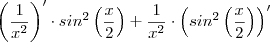
![\frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot \left(sin \left(\frac{x}{2}\right)\right)' \right] \frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot \left(sin \left(\frac{x}{2}\right)\right)' \right]](/latexrender/pictures/b714fc08b15c3e7cabbe23768d6ef967.png)
![\frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot cos\left(\frac{x}{2}\right)\cdot \left(\frac{x}{2}\right)' \right] \frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot cos\left(\frac{x}{2}\right)\cdot \left(\frac{x}{2}\right)' \right]](/latexrender/pictures/7adb9be375fc0eea770dd074e2c18f42.png)
![\frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot cos\left(\frac{x}{2}\right)\cdot \frac{2}{4} \right] \frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot cos\left(\frac{x}{2}\right)\cdot \frac{2}{4} \right]](/latexrender/pictures/137702bffa4660523cc604956e778581.png)
Será que está bem?Alguém pode conferir?
Isto de calcular a derivada complica-se quando é preciso misturar a regra do quociente, do produto e da cadeia.
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Qui Dez 01, 2011 01:45
por MarceloFantini » Qui Dez 01, 2011 01:45
Está certo, mas simplifique
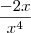
para
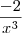
, não era necessário colocar

, embora não está errado a derivada de

é

, não havia necessidade de multiplicar numerador e denominador por 2.
Poderia ter notado que
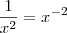
e então
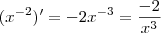
. Uma forma interessante seria notar que
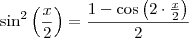
, daí
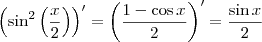
.
Note que é consistente, uma vez que
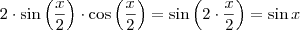
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Expressão Trigonométrica
por Anderson Alves » Dom Mar 04, 2012 22:21
- 2 Respostas
- 1897 Exibições
- Última mensagem por Anderson Alves

Dom Mar 04, 2012 23:27
Trigonometria
-
- Expressão Trigonométrica
por Pri Ferreira » Seg Abr 09, 2012 15:44
- 1 Respostas
- 1339 Exibições
- Última mensagem por LuizAquino

Sex Abr 13, 2012 12:56
Trigonometria
-
- Expressão Trigonométrica
por Man Utd » Sáb Jun 15, 2013 20:45
- 0 Respostas
- 851 Exibições
- Última mensagem por Man Utd

Sáb Jun 15, 2013 20:45
Trigonometria
-
- [Trigonometria] Expressão trigonométrica
por Kleveland Cristian » Seg Abr 30, 2012 12:48
- 3 Respostas
- 5068 Exibições
- Última mensagem por DanielFerreira

Ter Mai 01, 2012 15:02
Trigonometria
-
- Trigonometria: Cálculo da Expressão Trigonométrica
por leotecco » Qui Mai 21, 2015 19:59
- 0 Respostas
- 1791 Exibições
- Última mensagem por leotecco

Qui Mai 21, 2015 19:59
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
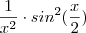
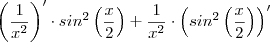
![\frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot \left(sin \left(\frac{x}{2}\right)\right)' \right] \frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot \left(sin \left(\frac{x}{2}\right)\right)' \right]](/latexrender/pictures/b714fc08b15c3e7cabbe23768d6ef967.png)
![\frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot cos\left(\frac{x}{2}\right)\cdot \left(\frac{x}{2}\right)' \right] \frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot cos\left(\frac{x}{2}\right)\cdot \left(\frac{x}{2}\right)' \right]](/latexrender/pictures/7adb9be375fc0eea770dd074e2c18f42.png)
![\frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot cos\left(\frac{x}{2}\right)\cdot \frac{2}{4} \right] \frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot cos\left(\frac{x}{2}\right)\cdot \frac{2}{4} \right]](/latexrender/pictures/137702bffa4660523cc604956e778581.png)

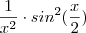
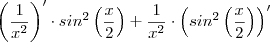
![\frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot \left(sin \left(\frac{x}{2}\right)\right)' \right] \frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot \left(sin \left(\frac{x}{2}\right)\right)' \right]](/latexrender/pictures/b714fc08b15c3e7cabbe23768d6ef967.png)
![\frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot cos\left(\frac{x}{2}\right)\cdot \left(\frac{x}{2}\right)' \right] \frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot cos\left(\frac{x}{2}\right)\cdot \left(\frac{x}{2}\right)' \right]](/latexrender/pictures/7adb9be375fc0eea770dd074e2c18f42.png)
![\frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot cos\left(\frac{x}{2}\right)\cdot \frac{2}{4} \right] \frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot cos\left(\frac{x}{2}\right)\cdot \frac{2}{4} \right]](/latexrender/pictures/137702bffa4660523cc604956e778581.png)

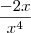 para
para 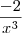 , não era necessário colocar
, não era necessário colocar  , embora não está errado a derivada de
, embora não está errado a derivada de  é
é  , não havia necessidade de multiplicar numerador e denominador por 2.
, não havia necessidade de multiplicar numerador e denominador por 2. 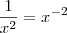 e então
e então 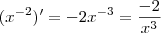 . Uma forma interessante seria notar que
. Uma forma interessante seria notar que 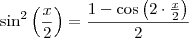 , daí
, daí 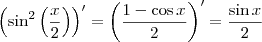 .
. 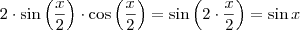 .
.

