 por Fernandadb » Seg Nov 28, 2011 14:55
por Fernandadb » Seg Nov 28, 2011 14:55
Não sei resolver está questão,Calcule as integrais usando os principais teoremas de
integração e a fórmula
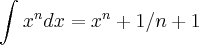
+ k, sendo k
constante.
![\int_{}^{} x + 1/\sqrt[4]{}x^5 \int_{}^{} x + 1/\sqrt[4]{}x^5](/latexrender/pictures/2e1587d3c77eca9c2582781f3df71f16.png)
Consegui termina não sei se está certo-
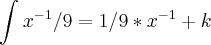
Obrigada pela ajuda!!

Editado pela última vez por
Fernandadb em Seg Nov 28, 2011 18:26, em um total de 2 vezes.
-
Fernandadb
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Nov 28, 2011 14:22
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Seg Nov 28, 2011 17:34
por LuizAquino » Seg Nov 28, 2011 17:34
Fernandadb escreveu:Não sei resolver está questão, Calcule as integrais usando os principais teoremas de
integração e a fórmula
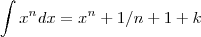
, sendo k
constante.
![\int x + 1/\sqrt[4]{}x^5 \int x + 1/\sqrt[4]{}x^5](/latexrender/pictures/851b790ba926e0f935d55f38137c1864.png)
Apenas arrumando a fórmula:
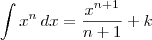
Vale lembrar que essa fórmula só é válida para
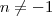
.
Do jeito que você escreveu, o exercício seria algo como:
![\int x + \frac{1}{\sqrt[4]{x^5}} \,dx \int x + \frac{1}{\sqrt[4]{x^5}} \,dx](/latexrender/pictures/dbe3a82f65f49df4b88f52506bb1998d.png)
Nesse caso, basta lembrar que:
![\int x + \frac{1}{\sqrt[4]{x^5}} \,dx = \int x \,dx + \int x^{-\frac{5}{4}} \,dx \int x + \frac{1}{\sqrt[4]{x^5}} \,dx = \int x \,dx + \int x^{-\frac{5}{4}} \,dx](/latexrender/pictures/79aafb026bd970028ad7fc361c73f34c.png)
Por outro lado, considerando que você tenha errado na digitação, o exercício seria algo como:
![\int \frac{x+1}{\sqrt[4]{x^5}} \,dx \int \frac{x+1}{\sqrt[4]{x^5}} \,dx](/latexrender/pictures/e3d00853756908689b42f2cf9bbc7082.png)
Se esse for o caso, então basta lembrar que:
![\int \frac{x+1}{\sqrt[4]{x^5}} \,dx = \int \frac{x}{\sqrt[4]{x^5}} \,dx + \int \frac{1}{\sqrt[4]{x^5}} \,dx \int \frac{x+1}{\sqrt[4]{x^5}} \,dx = \int \frac{x}{\sqrt[4]{x^5}} \,dx + \int \frac{1}{\sqrt[4]{x^5}} \,dx](/latexrender/pictures/1dda602b73dedd72935bbf371fa156d6.png)
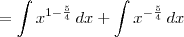
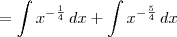
Agora tente terminar o exercício.
Editado pela última vez por
LuizAquino em Ter Nov 29, 2011 09:51, em um total de 1 vez.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Estou com dificuldade para resolver esta integral
por Paulo Perez » Qui Out 03, 2013 12:22
- 2 Respostas
- 4623 Exibições
- Última mensagem por Paulo Perez

Sex Out 04, 2013 16:32
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4591 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4350 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Qua Ago 17, 2011 22:33
- 2 Respostas
- 2853 Exibições
- Última mensagem por ewald

Qui Ago 18, 2011 00:54
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Sáb Ago 20, 2011 17:20
- 2 Respostas
- 2882 Exibições
- Última mensagem por LuizAquino

Dom Ago 21, 2011 21:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
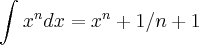 + k, sendo k
+ k, sendo k![\int_{}^{} x + 1/\sqrt[4]{}x^5 \int_{}^{} x + 1/\sqrt[4]{}x^5](/latexrender/pictures/2e1587d3c77eca9c2582781f3df71f16.png)
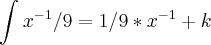


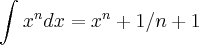 + k, sendo k
+ k, sendo k![\int_{}^{} x + 1/\sqrt[4]{}x^5 \int_{}^{} x + 1/\sqrt[4]{}x^5](/latexrender/pictures/2e1587d3c77eca9c2582781f3df71f16.png)
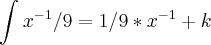


, sendo k
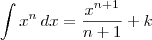
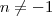 .
.![\int x + \frac{1}{\sqrt[4]{x^5}} \,dx \int x + \frac{1}{\sqrt[4]{x^5}} \,dx](/latexrender/pictures/dbe3a82f65f49df4b88f52506bb1998d.png)
![\int x + \frac{1}{\sqrt[4]{x^5}} \,dx = \int x \,dx + \int x^{-\frac{5}{4}} \,dx \int x + \frac{1}{\sqrt[4]{x^5}} \,dx = \int x \,dx + \int x^{-\frac{5}{4}} \,dx](/latexrender/pictures/79aafb026bd970028ad7fc361c73f34c.png)
![\int \frac{x+1}{\sqrt[4]{x^5}} \,dx \int \frac{x+1}{\sqrt[4]{x^5}} \,dx](/latexrender/pictures/e3d00853756908689b42f2cf9bbc7082.png)
![\int \frac{x+1}{\sqrt[4]{x^5}} \,dx = \int \frac{x}{\sqrt[4]{x^5}} \,dx + \int \frac{1}{\sqrt[4]{x^5}} \,dx \int \frac{x+1}{\sqrt[4]{x^5}} \,dx = \int \frac{x}{\sqrt[4]{x^5}} \,dx + \int \frac{1}{\sqrt[4]{x^5}} \,dx](/latexrender/pictures/1dda602b73dedd72935bbf371fa156d6.png)
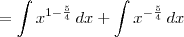
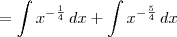

![\int x + \frac{1}{\sqrt[4]{x^5}} \,dx \int x + \frac{1}{\sqrt[4]{x^5}} \,dx](/latexrender/pictures/dbe3a82f65f49df4b88f52506bb1998d.png) , temos que:
, temos que:![\int x + \frac{1}{\sqrt[4]{x^5}} \,dx = \int x \,dx + \int x^{-\frac{5}{4}} \,dx \int x + \frac{1}{\sqrt[4]{x^5}} \,dx = \int x \,dx + \int x^{-\frac{5}{4}} \,dx](/latexrender/pictures/79aafb026bd970028ad7fc361c73f34c.png)
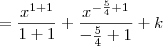
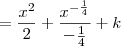
![= \frac{x^2}{2} - \frac{4}{\sqrt[4]{x}} + k = \frac{x^2}{2} - \frac{4}{\sqrt[4]{x}} + k](/latexrender/pictures/7644e24a3a0299878dabde9b4191d539.png)
![\int \frac{x+1}{\sqrt[4]{x^5}} \,dx \int \frac{x+1}{\sqrt[4]{x^5}} \,dx](/latexrender/pictures/e3d00853756908689b42f2cf9bbc7082.png) , temos que:
, temos que:![\int \frac{x+1}{\sqrt[4]{x^5}} \,dx = \int x^{-\frac{1}{4}} \, dx + \int x^{-\frac{5}{4}} \,dx \int \frac{x+1}{\sqrt[4]{x^5}} \,dx = \int x^{-\frac{1}{4}} \, dx + \int x^{-\frac{5}{4}} \,dx](/latexrender/pictures/b14366304418b10d016e47a7f6cb7287.png)
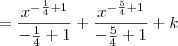
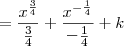
![= \frac{4}{3}\sqrt[4]{x^3} - \frac{4}{\sqrt[4]{x}} + k = \frac{4}{3}\sqrt[4]{x^3} - \frac{4}{\sqrt[4]{x}} + k](/latexrender/pictures/33b91253e6675aaf9ffd035ff3c7e927.png)
