 por beel » Dom Nov 27, 2011 18:24
por beel » Dom Nov 27, 2011 18:24
nessa integral
![\int_{}^{}\frac{2dt}{\sqrt[]{t}+ 4t\sqrt[]{t}} \int_{}^{}\frac{2dt}{\sqrt[]{t}+ 4t\sqrt[]{t}}](/latexrender/pictures/9c6754ce7f46b31bd4a926bf0f5d5bd4.png)
tentei colocar o denominador como uma soma pra fazer a substituiçao trigonometrica, e ficou assim:
![\int_{}^{}\frac{2dt d\theta}{\sqrt[]{t}(1+ 4t)} \int_{}^{}\frac{2dt d\theta}{\sqrt[]{t}(1+ 4t)}](/latexrender/pictures/0258a3e5540c27a2c16b0d220f3a7300.png)
...
travei de novo e cheguei ate esse resultado
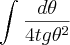
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Seg Nov 28, 2011 16:24
por LuizAquino » Seg Nov 28, 2011 16:24
beel escreveu:essa integral
![\int_{}^{}\frac{2dt}{\sqrt[]{t}+ 4t\sqrt[]{t}} \int_{}^{}\frac{2dt}{\sqrt[]{t}+ 4t\sqrt[]{t}}](/latexrender/pictures/9c6754ce7f46b31bd4a926bf0f5d5bd4.png)
tentei colocar o denominador como uma soma pra fazer a substituiçao trigonometrica, e ficou assim:
![\int_{}^{}\frac{2dt d\theta}{\sqrt[]{t}(1+ 4t)} \int_{}^{}\frac{2dt d\theta}{\sqrt[]{t}(1+ 4t)}](/latexrender/pictures/0258a3e5540c27a2c16b0d220f3a7300.png)
...
travei de novo e cheguei ate esse resultado
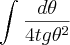
Para conferir sua resolução, basta seguir os procedimentos abaixo.
- Acesse a página: http://www.wolframalpha.com/
- No campo de entrada, digite:
- Código: Selecionar todos
integrate 2/(sqrt(t) + (4t)*sqrt(t)) dt
- Clique no botão de igual ao lado do campo de entrada.
- Após a integral ser calculada, clique no botão "Show steps" ao lado do resultado.
- Pronto! Agora basta estudar a resolução e comparar com a sua.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Seg Nov 28, 2011 16:35
por beel » Seg Nov 28, 2011 16:35
Gostei do site,uso pra conferir respostas mais diretas, mas essas que eu posto aqui nao consegui resolver olhando o site e gostaria de ajuda, voces sempre sugerem esse site, e sei que ele existe agora, e se ainda sim postei minha duvida quer dizer que nao resolveu, mas ok, obrigada...
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Seg Nov 28, 2011 16:44
por LuizAquino » Seg Nov 28, 2011 16:44
beel escreveu:Gostei do site, uso pra conferir respostas mais diretas, mas essas que eu posto aqui nao consegui resolver olhando o site e gostaria de ajuda, voces sempre sugerem esse site, e sei que ele existe agora, e se ainda sim postei minha duvida quer dizer que nao resolveu, mas ok, obrigada...
Seguindo os procedimentos acima, obtemos o texto abaixo. Em que parte você tem dificuldade?
Possible intermediate steps:
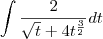
Factor out constants:
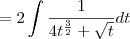
For the integrand
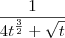
, substitute

and
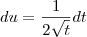
:
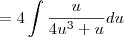
For the integrand
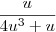
, cancel common terms in the numerator and denominator:
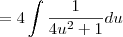
The integral of
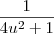
is
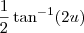
:
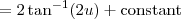
Substitute back for

:
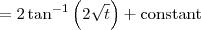
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral por substituição trigonométrica.
por ClaudioSP » Qui Out 08, 2009 12:25
- 1 Respostas
- 3762 Exibições
- Última mensagem por ClaudioSP

Qui Out 08, 2009 14:25
Cálculo: Limites, Derivadas e Integrais
-
- integral- substituiçao trigonometrica 4
por beel » Dom Nov 27, 2011 18:29
- 1 Respostas
- 2068 Exibições
- Última mensagem por LuizAquino

Seg Nov 28, 2011 16:26
Cálculo: Limites, Derivadas e Integrais
-
- Integral por substituição trigonométrica
por Crist » Seg Nov 12, 2012 20:46
- 1 Respostas
- 1495 Exibições
- Última mensagem por e8group

Qui Nov 15, 2012 15:38
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Substituição Trigonométrica
por klueger » Qua Mar 06, 2013 23:03
- 4 Respostas
- 3679 Exibições
- Última mensagem por Russman

Qui Mar 07, 2013 01:45
Cálculo: Limites, Derivadas e Integrais
-
- integral substituição trigonométrica
por samysoares » Dom Mai 26, 2013 17:13
- 1 Respostas
- 1364 Exibições
- Última mensagem por e8group

Dom Mai 26, 2013 19:36
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{}^{}\frac{2dt}{\sqrt[]{t}+ 4t\sqrt[]{t}} \int_{}^{}\frac{2dt}{\sqrt[]{t}+ 4t\sqrt[]{t}}](/latexrender/pictures/9c6754ce7f46b31bd4a926bf0f5d5bd4.png)
![\int_{}^{}\frac{2dt d\theta}{\sqrt[]{t}(1+ 4t)} \int_{}^{}\frac{2dt d\theta}{\sqrt[]{t}(1+ 4t)}](/latexrender/pictures/0258a3e5540c27a2c16b0d220f3a7300.png)
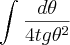

![\int_{}^{}\frac{2dt}{\sqrt[]{t}+ 4t\sqrt[]{t}} \int_{}^{}\frac{2dt}{\sqrt[]{t}+ 4t\sqrt[]{t}}](/latexrender/pictures/9c6754ce7f46b31bd4a926bf0f5d5bd4.png)
![\int_{}^{}\frac{2dt d\theta}{\sqrt[]{t}(1+ 4t)} \int_{}^{}\frac{2dt d\theta}{\sqrt[]{t}(1+ 4t)}](/latexrender/pictures/0258a3e5540c27a2c16b0d220f3a7300.png)
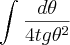



, substitute
and
:
, cancel common terms in the numerator and denominator:
is
:
:
