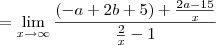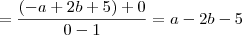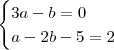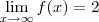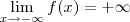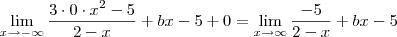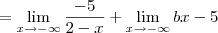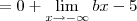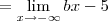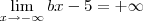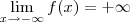por carvalhothg » Qua Nov 23, 2011 12:04
por carvalhothg » Qua Nov 23, 2011 12:04
Como resolvo este limite para encontrar os valores de a e b. Não estou conseguindo, sempre chego na indeterminação de

- Se
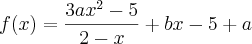
, calcule a e b de modo que:
1)
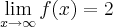
2)
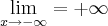
-
carvalhothg
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Dom Set 04, 2011 18:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [LIMITES] Me ajudem
por carvalhothg » Qua Nov 16, 2011 16:52
- 2 Respostas
- 1254 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 19:26
Cálculo: Limites, Derivadas e Integrais
-
- LIMITES ME AJUDEM POR FAVOR URGENTE
por gaahbr » Qui Nov 07, 2013 11:47
- 0 Respostas
- 1933 Exibições
- Última mensagem por gaahbr

Qui Nov 07, 2013 11:47
Cálculo: Limites, Derivadas e Integrais
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 5411 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]Preciso de ajuda para calcular alguns limites
por Pessoa Estranha » Ter Jul 16, 2013 17:15
- 2 Respostas
- 4759 Exibições
- Última mensagem por LuizAquino

Qua Jul 17, 2013 09:12
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Ajuda com limites no infinito e continuidade
 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4786 Exibições
- Última mensagem por umbrorz

Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

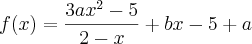 , calcule a e b de modo que:
, calcule a e b de modo que: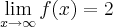
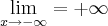


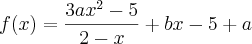 , calcule a e b de modo que:
, calcule a e b de modo que: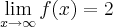
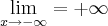

, calcule a e b de modo que:
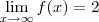
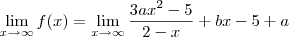
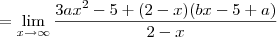
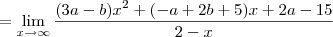
![\lim_{x\to \infty} \frac{(- a + 2b + 5)x + 2a - 15}{2-x} = \lim_{x\to \infty} \frac{[(- a + 2b + 5)x + 2a - 15]:x}{(2-x):x} \lim_{x\to \infty} \frac{(- a + 2b + 5)x + 2a - 15}{2-x} = \lim_{x\to \infty} \frac{[(- a + 2b + 5)x + 2a - 15]:x}{(2-x):x}](/latexrender/pictures/510cc53bdff32e22684e38d72ddf7cc9.png)