 por quantun » Qua Mai 20, 2009 16:29
por quantun » Qua Mai 20, 2009 16:29
olar, eu tive 1 test hj e me deparei com esta questao;
dada a funçao f(x)=[arsen(-2x²-x)+2]³
a)calcule g(0)
b)calcule g' (0)
eu tentei 2 formas diferentes uma usando a derivada dy/du que deu 2 respostas uma = a "9x.arcsen(-2x²-x)cos(-2x²-x)" e outra = a "32x.arcsen(-2x)cos(-2x)" e a segunda forma de calculo deu a seguinte resposta g(0)=5arcsen(-2x)isso usando a regra do tombo, mas nao estou satisfeito com os resultados.
alguem poderia me dar uma segunda opniao?
Editado pela última vez por
quantun em Qui Mai 21, 2009 02:43, em um total de 1 vez.
-
quantun
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Mai 20, 2009 16:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: BACHARELADO EM FISICA
- Andamento: cursando
 por quantun » Qua Mai 20, 2009 16:36
por quantun » Qua Mai 20, 2009 16:36
texto removido
Editado pela última vez por
quantun em Qui Mai 21, 2009 02:46, em um total de 1 vez.
-
quantun
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Mai 20, 2009 16:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: BACHARELADO EM FISICA
- Andamento: cursando
 por Molina » Qui Mai 21, 2009 01:44
por Molina » Qui Mai 21, 2009 01:44
Boa noite.
Acho que aqui você terá que realmente fazer a regra da cadeia..
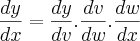
, sendo:
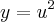
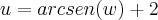
e

Abraços e bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por quantun » Qui Mai 21, 2009 02:41
por quantun » Qui Mai 21, 2009 02:41
ta mais e o que eu faço com esta potencia do lado de fora dos colchetes?
e ufiz assim:
regra do tombo: g(0)= [arcsen(-2x²-x)+2]³ ==>> 3arcsen(-2x)+2 logo dy/dx = dy/dv . dv/dw . dw/dx sendo,
f'(u)=3arcsen(u)+2 e g'(x)=(-2x) assim,
F'(x)=f'(g(x)).g'(x)
=3arccos(-2x)+2
=5arccos(-2x) <<<<<<<<<resposta final
esta correto?
-
quantun
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Mai 20, 2009 16:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: BACHARELADO EM FISICA
- Andamento: cursando
 por Molina » Qui Mai 21, 2009 02:59
por Molina » Qui Mai 21, 2009 02:59
quantun escreveu:dada a funçao f(x)=[arsen(-2x²-x)+2]³
a)calcule g(0)
b)calcule g' (0)
(...)
Responde pra mim uma coisa antes:
Não seria pra calcular o f(0) e o f'(0) ao invés de calcular o g(0) e o g'(0)?


Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por quantun » Qui Mai 21, 2009 10:29
por quantun » Qui Mai 21, 2009 10:29
sim é g'(0) e g(0), ue qe errei ali na equaçao mas é cm g e nao com f
-
quantun
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Mai 20, 2009 16:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: BACHARELADO EM FISICA
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12556 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10896 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Com duas variáveis e derivada mista
por leticiaeverson » Dom Abr 22, 2018 00:39
- 3 Respostas
- 13201 Exibições
- Última mensagem por Gebe

Dom Abr 22, 2018 17:11
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14807 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] DERIVADA POR DEFINIÇÃO DA RAIZ DO MÓDULO DE X
por Matheusgdp » Qua Set 16, 2015 04:07
- 2 Respostas
- 5116 Exibições
- Última mensagem por Matheusgdp

Qui Set 17, 2015 18:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


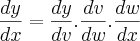 , sendo:
, sendo:
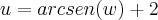






 .
.



