 por barbaradaiprai » Dom Nov 20, 2011 18:06
por barbaradaiprai » Dom Nov 20, 2011 18:06
oi, alguém pode me ajudar nessas questoes??
fico grata
1)Para cada função determinar:
a) Os zeros da função, caso existam;
b) O vértice da função;
c) Como é a concavidade da função e se o vértice é ponto de máximo ou de mínimo;
d) Representação gráfica
e) Domínio e Imagem da função
1) y= x2 +12x +36
2) y= -x2 -x +6
3) y= x2 +3x +7
2)Um terreno de forma retangular tem perímetro igual a 60 m.
a)Expresse a área desse terreno em função do comprimento de um dos lados.
b)Construa o gráfico dessa função.
c)Calcule as dimensões desse terreno para que a área seja máxima.
-
barbaradaiprai
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Nov 06, 2011 21:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por MarceloFantini » Dom Nov 20, 2011 19:12
por MarceloFantini » Dom Nov 20, 2011 19:12
Quais foram suas tentativas?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por barbaradaiprai » Dom Nov 20, 2011 20:15
por barbaradaiprai » Dom Nov 20, 2011 20:15
A numero um, eu consegui fazer!
a 2 que ficou divifil
será que a Area é = 200m??
o resto não consegui!
-
barbaradaiprai
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Nov 06, 2011 21:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por MarceloFantini » Dom Nov 20, 2011 20:39
por MarceloFantini » Dom Nov 20, 2011 20:39
O perímetro é a soma de todos os lados do polígono. Se chamar um lado de x e a altura de y, teremos que pela simetria o perímetro é
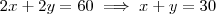
. A área é simplesmente base vezes altura, daí

. Mas podemos isolar um deles, por exemplo
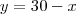
e daí
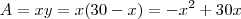
. Para encontrar a área máxima use o vértice da parábola. Tente terminar.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função quadrática
por Ananda » Sex Mar 28, 2008 16:00
- 6 Respostas
- 9240 Exibições
- Última mensagem por admin

Sex Mar 28, 2008 21:25
Funções
-
- Função quadratica
por Aline » Qui Jun 18, 2009 14:22
- 2 Respostas
- 2634 Exibições
- Última mensagem por Cleyson007

Sex Jun 19, 2009 10:00
Funções
-
- Função Quadratica
por Aline » Qui Jun 18, 2009 14:37
- 1 Respostas
- 2016 Exibições
- Última mensagem por Marcampucio

Qui Jun 18, 2009 16:45
Funções
-
- Função Quadratica
por Aline » Sáb Jun 20, 2009 18:23
- 1 Respostas
- 2094 Exibições
- Última mensagem por Molina

Dom Jun 21, 2009 20:28
Funções
-
- Função Quadratica
 por guijermous » Sáb Abr 10, 2010 10:02
por guijermous » Sáb Abr 10, 2010 10:02
- 4 Respostas
- 8042 Exibições
- Última mensagem por Molina

Sáb Abr 10, 2010 16:27
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




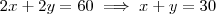 . A área é simplesmente base vezes altura, daí
. A área é simplesmente base vezes altura, daí  . Mas podemos isolar um deles, por exemplo
. Mas podemos isolar um deles, por exemplo 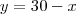 e daí
e daí 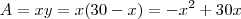 . Para encontrar a área máxima use o vértice da parábola. Tente terminar.
. Para encontrar a área máxima use o vértice da parábola. Tente terminar.