 por carvalhothg » Qui Nov 17, 2011 11:29
por carvalhothg » Qui Nov 17, 2011 11:29
Mostre que a equação abaixo possui uma unica solução e que essa solução pertence ao intervalo

.

Pessoal como encontro este intervalo, pois eu consegui encontrar somente o dominio da função que é

-
carvalhothg
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Dom Set 04, 2011 18:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por MarceloFantini » Qui Nov 17, 2011 14:34
por MarceloFantini » Qui Nov 17, 2011 14:34
Considere a função
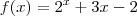
. Encontre dois valores no intervalo

tais que um deles a função seja negativa e no outro a função seja positiva. Pelo teorema do anulamento existe um valor que tal que a função se anula (pois ela é contínua).
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por carvalhothg » Qui Nov 17, 2011 20:44
por carvalhothg » Qui Nov 17, 2011 20:44
O que o prof. esta querendo dizer, quando ele cita que a equação tem uma unica solução?
E porque esta solução deve pertencer ao intervalo de

.
Ainda continuo não entendendo.
-
carvalhothg
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Dom Set 04, 2011 18:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por MarceloFantini » Qui Nov 17, 2011 20:49
por MarceloFantini » Qui Nov 17, 2011 20:49
Ter solução significa que existe um valor que faz a igualdade ser verdadeira. Se é única, só existe aquele valor. A solução pertencer ao intervalo significa que ela não pode estar em outro lugar.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por carvalhothg » Qui Nov 17, 2011 21:03
por carvalhothg » Qui Nov 17, 2011 21:03
Então neste exercício eu vou ter que igualar a função igual a zero e encontrar o valor de x?
É isto que devo fazer para concluir este exercício?
-
carvalhothg
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Dom Set 04, 2011 18:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por MarceloFantini » Qui Nov 17, 2011 21:06
por MarceloFantini » Qui Nov 17, 2011 21:06
Em teoria, sim. Na prática, você não vai conseguir um solução exata. Mas você não precisa. Carvalho, releia a primeira mensagem.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por carvalhothg » Qui Nov 17, 2011 21:38
por carvalhothg » Qui Nov 17, 2011 21:38
Bom na primeira menssagem tu disse que é para considerar a função:

E encontrar dois valores no intervalo tais que um deles a função seja negativa e no outro a função seja positiva.
Bom, levantando o gráfico da função citada eu não encontrei valores positivos neste intervalo entre 0 e 2/3, pois a função só tera valor positivo

O que você me diz a respeito?
-
carvalhothg
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Dom Set 04, 2011 18:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [FUNÇÕES]Ajudem
por Miya » Sex Abr 17, 2015 09:17
- 0 Respostas
- 748 Exibições
- Última mensagem por Miya

Sex Abr 17, 2015 09:17
Funções
-
- funções(ajudem por favor!!)
por pauloleigo » Sex Set 16, 2011 03:36
- 1 Respostas
- 1368 Exibições
- Última mensagem por Neperiano

Sex Set 16, 2011 15:28
Funções
-
- [funções]ME AJUDEM POR FAVOR
por Miya » Dom Abr 05, 2015 13:06
- 3 Respostas
- 1768 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 25, 2015 22:31
Funções
-
- Funções quadraticas pf me ajudem
por Thalia Cristina » Qui Nov 05, 2015 21:03
- 1 Respostas
- 3194 Exibições
- Última mensagem por nakagumahissao

Sex Nov 06, 2015 10:24
Funções
-
- Funções quadraticas pf me ajudem
por Thalia Cristina » Qui Nov 05, 2015 19:39
- 1 Respostas
- 2089 Exibições
- Última mensagem por nakagumahissao

Sex Nov 06, 2015 10:38
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 .
.


 .
.


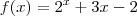 . Encontre dois valores no intervalo
. Encontre dois valores no intervalo  tais que um deles a função seja negativa e no outro a função seja positiva. Pelo teorema do anulamento existe um valor que tal que a função se anula (pois ela é contínua).
tais que um deles a função seja negativa e no outro a função seja positiva. Pelo teorema do anulamento existe um valor que tal que a função se anula (pois ela é contínua).

 .
.










![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.