A dúvida é a seguinte :
Numa EDO não homogênea de segunda ordem, da forma a(x) y''+ b(x) y' + c(x) y = d(x) , onde o d(x) possui uma função trigonométrica. Como eu procedo na resolução ? Tenho uma resposta "pronta" aqui ,ela está escrita na seguinte forma genérica :
Se d(x) está na forma :
![d(x)= {e}^{u*x}[{P}_{n}(x)*cos(v*x) + {Q}_{m}(x)*sen(v*x)]](/latexrender/pictures/17426d408e7d6e6fb7d09078a5588de4.png "d(x)= {e}^{u*x}[{P}_{n}(x)*cos(v*x) + {Q}_{m}(x)*sen(v*x)]")
, onde P e Q são polinomios de grau n e m respectivamente Casos de resposta :
1°. u+- i*v não é raiz da equação característica ------->
![{y}_{n}(x) = {e}^{u*x}[{S}_{M}(x)*cos(v*x) + {T}_{M}(x)*sen(v*x)]](/latexrender/pictures/356fd45de7f313322dcfea58e0534e77.png "{y}_{n}(x) = {e}^{u*x}[{S}_{M}(x)*cos(v*x) + {T}_{M}(x)*sen(v*x)]")
, M= max {m,n}2°. u +- i*v é raiz da equação característica -------->
![{y}_{n}(x) = x*{e}^{u*x}[{S}_{M}(x)*cos(v*x) + {T}_{M}(x)*sen(v*x)]](/latexrender/pictures/7c343fd706491b022144e9a6dce1ad73.png "{y}_{n}(x) = x*{e}^{u*x}[{S}_{M}(x)*cos(v*x) + {T}_{M}(x)*sen(v*x)]")
, M= max {m,n}A pergunta é .... o que DIABOS 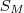é
e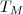 
? E o que é o "M= max {m,n}" ? Sei que é uma resolução feita e muita gente pode nao resolver desse jeito, mas é o que eu tenho pra resolver !Valeu !
, avisa que eu resolvo.
