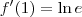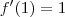por joaofonseca » Ter Nov 08, 2011 12:04
por joaofonseca » Ter Nov 08, 2011 12:04
Tenho estado a estudar uma abordagem às derivadas do ponto de vista do declive da reta secante a dois pontos.Calculando o limite desse mesmo declive num ponto.
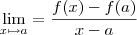
Quando

o declive da reta secante aproxima-se do declive da reta tangente a
a.Ou seja do valor da derivada no ponto x=a.
Quando o calculo do limite não corre bem, as coisas começam a complicar-se!
Seja a função
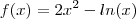
. Calcule-se o declive da reta tangente no ponto (1,2), utilizando a primeira formula:
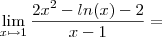
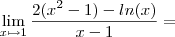
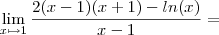
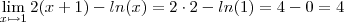
Seria de concluir que a derivada da função no ponto x=1 seria 4!!!
Mas quando calculo a derivada através das regras de diferenciação obtenho:
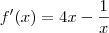
ou seja,
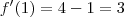
Em qual deles errei?
Após algumas simulações gráficas, verifiquei que foi no limite que errei, mas por mais que me esforce não sei onde.Podem ajudar-me?
Obrigado
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Ter Nov 08, 2011 16:31
por MarceloFantini » Ter Nov 08, 2011 16:31
Você dividiu apenas o lado direito por x-1, e não tudo. O resultado deveria ser o limite de
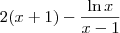
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por joaofonseca » Ter Nov 08, 2011 17:30
por joaofonseca » Ter Nov 08, 2011 17:30
Obrigado! Não estava mesmo exergando.
No entanto mesmo assim o resultado do limite continua na mesma, pois
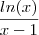
resulta em

quando se substituí
x por 1.
Foi então, que após alguma pesquisa, e no seguimento da definição de derivada que estou a utilizar, descobri:
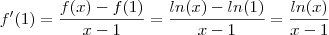
Ou seja a expressão reflete a derivada da função ln(x) no ponto x=1.E como sabemos, será igual a 1.
Assim:
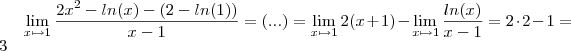
Agora sim, coincide com o valor que obtive através das regras de diferenciação!!!!
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Sex Nov 11, 2011 10:30
por LuizAquino » Sex Nov 11, 2011 10:30
joaofonseca escreveu:Foi então, que após alguma pesquisa, e no seguimento da definição de derivada que estou a utilizar, descobri:
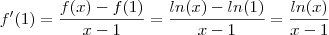
Correção:
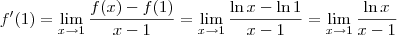
Para calcular esse limite, faça a substituição
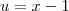
. Como
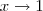
, teremos que
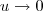
. Portanto, podemos escrever:
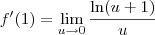
Note que podemos ainda escrever:
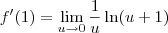
Utilizando propriedades de logaritmo, temos que:
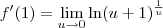
Como a função logaritmo natural é contínua em u+1 quando
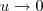
, o limite poderá "entrar" na função:
![f^\prime(1) =\ln \left[\lim_{u\to 0} (u+1)^{\frac{1}{u}}\right] f^\prime(1) =\ln \left[\lim_{u\to 0} (u+1)^{\frac{1}{u}}\right]](/latexrender/pictures/154d10a29b8f7b0bba9e026f2e5b1a43.png)
Lembrando-se do limite exponencial fundamental, temos que:
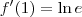
Portanto, como já era esperado, obtemos que:
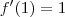
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [circunferência] Questão de reta secante a circunferência
por danielleecb » Qui Jun 07, 2012 23:26
- 1 Respostas
- 1876 Exibições
- Última mensagem por MarceloFantini

Sex Jun 08, 2012 12:24
Geometria Analítica
-
- O declive de origem ordenada
por Midelio12 » Seg Ago 13, 2018 15:07
- 0 Respostas
- 4906 Exibições
- Última mensagem por Midelio12

Seg Ago 13, 2018 15:07
Álgebra Elementar
-
- Derivada de secante.
por Sobreira » Ter Nov 27, 2012 16:38
- 3 Respostas
- 2953 Exibições
- Última mensagem por MarceloFantini

Ter Nov 27, 2012 22:27
Cálculo: Limites, Derivadas e Integrais
-
- Demonstração- secante
 por mathsoliver » Seg Abr 13, 2015 12:32
por mathsoliver » Seg Abr 13, 2015 12:32
- 1 Respostas
- 1758 Exibições
- Última mensagem por Cleyson007

Seg Abr 13, 2015 16:51
Equações
-
- seno e secante negativa
por Apotema » Seg Nov 23, 2009 14:36
- 2 Respostas
- 1987 Exibições
- Última mensagem por Apotema

Qua Nov 25, 2009 16:54
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
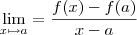
 o declive da reta secante aproxima-se do declive da reta tangente a a.Ou seja do valor da derivada no ponto x=a.
o declive da reta secante aproxima-se do declive da reta tangente a a.Ou seja do valor da derivada no ponto x=a.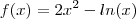 . Calcule-se o declive da reta tangente no ponto (1,2), utilizando a primeira formula:
. Calcule-se o declive da reta tangente no ponto (1,2), utilizando a primeira formula: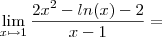
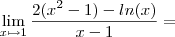
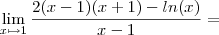
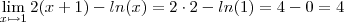
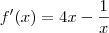
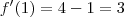


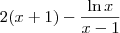 .
.

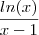 resulta em
resulta em  quando se substituí
quando se substituí 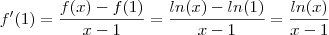
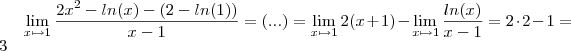
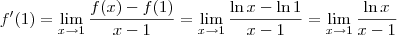
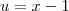 . Como
. Como 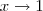 , teremos que
, teremos que 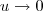 . Portanto, podemos escrever:
. Portanto, podemos escrever: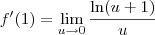
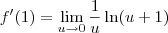
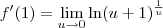
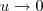 , o limite poderá "entrar" na função:
, o limite poderá "entrar" na função:![f^\prime(1) =\ln \left[\lim_{u\to 0} (u+1)^{\frac{1}{u}}\right] f^\prime(1) =\ln \left[\lim_{u\to 0} (u+1)^{\frac{1}{u}}\right]](/latexrender/pictures/154d10a29b8f7b0bba9e026f2e5b1a43.png)