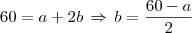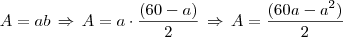por barbaradaiprai » Dom Nov 06, 2011 21:51
por barbaradaiprai » Dom Nov 06, 2011 21:51
Oiii
Eu preciso que alguém em ajude a como eu desenvolvo esta questão.
Quero construir uma quadra de futebol de salão retangular. Para cercá-la, disponho de 60m de alambrado pré-fabricado, e, por uma questão de economia, devo aproveitar o muro do quintal. A partir disso:
a) determine a área do cercado em função de um dos lados.
b) construa o gráfico dessa função.
c) verifique as dimensões para que o terreno tenha área máxima.
Por favor, se alguém souber, me ajude;
-
barbaradaiprai
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Nov 06, 2011 21:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Renato_RJ » Seg Nov 07, 2011 10:00
por Renato_RJ » Seg Nov 07, 2011 10:00
Bom dia Bárbara !! Tudo bem ??
Vejamos se posso lhe ajudar.. Esse me parece um típico problema de otimização...
Sejam a e b os lados da sua cerca, como você irá utilizar o muro como um lado também (por economia) então o seu perímetro será
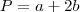
, logo temos:
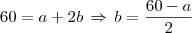
A sua área será:
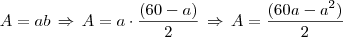
Aqui já temos a área em função de um dos lados (letra a), o gráfico é fácil verificar que será uma parábola com vértice em (30,450), sendo que sua concavidade é para baixo, pois o coeficiente líder da parábola é negativo...
As dimensões para que o terreno tenha área máxima você pode resolver de duas formas, uma é usando o cálculo (faça a derivada da área em função de a e estude seu sinal para achar o ponto de máximo da função) ou, simplesmente, perceba que o vértice já é o ponto de máximo da sua função, sendo a = 30 para uma área máxima, mas essa análise usando o vértice só vale pois o vértice está no primeiro quadrante (isto é, a é positivo), caso contrário teria que derivar a área em função de a para saber o ponto de máximo dentro do primeiro quadrante (isto é, seria um máximo local e não global como no caso do vértice).
Espero ter ajudado...
[ ] 's
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função quadrática
por Ananda » Sex Mar 28, 2008 16:00
- 6 Respostas
- 9243 Exibições
- Última mensagem por admin

Sex Mar 28, 2008 21:25
Funções
-
- Função quadratica
por Aline » Qui Jun 18, 2009 14:22
- 2 Respostas
- 2634 Exibições
- Última mensagem por Cleyson007

Sex Jun 19, 2009 10:00
Funções
-
- Função Quadratica
por Aline » Qui Jun 18, 2009 14:37
- 1 Respostas
- 2017 Exibições
- Última mensagem por Marcampucio

Qui Jun 18, 2009 16:45
Funções
-
- Função Quadratica
por Aline » Sáb Jun 20, 2009 18:23
- 1 Respostas
- 2096 Exibições
- Última mensagem por Molina

Dom Jun 21, 2009 20:28
Funções
-
- Função Quadratica
 por guijermous » Sáb Abr 10, 2010 10:02
por guijermous » Sáb Abr 10, 2010 10:02
- 4 Respostas
- 8042 Exibições
- Última mensagem por Molina

Sáb Abr 10, 2010 16:27
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


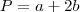 , logo temos:
, logo temos: