Sejam dois planos: x-y+2=0 e x+y+z=0
a)Determine equações paramétricas para a reta r interseção dos planos PI1 e PI2.
Achei os vetores normais do plano PI1 e PI2, são eles N1= (1, -1, 0) e N2= (1, 1, 1)
Depois fiz o produto vetorial de ambos para encontrar o vetor diretor
cheguei em (-i, -j, 2k)
Fiz um sistema
x-y+2=0
x+y+z=0
Atribui y=0
e encontrei o ponto P= (-1, 0, 1)
Eq. Paramétricas
x= -1-t
y= -t
z= 1+2t
b)Encontre uma equação geral do plano PI que é ortogonal a reta r e que passa pelo ponto P= (3, 5, 4)
Não consegui resolver a letra b


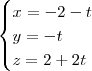
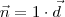 , podemos tomar o vetor normal
, podemos tomar o vetor normal 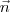 como sendo igual ao vetor diretor
como sendo igual ao vetor diretor 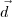 .
.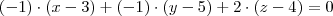


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)