 por Igor Mirandola » Sex Nov 04, 2011 00:55
por Igor Mirandola » Sex Nov 04, 2011 00:55
Vou supor que f eh uma função de R² em R, isso deveria ficar claro no enunciado...
vou supor ainda que (x,y) leva a f(x,y)...
Admitindo que, para todo (x,y)
4y. df/dx (x,y) - x df/dy(x,y) = 2
Calcule g' (t), sendo g(t) = f( 2cost, sent).
Agora observe que g(t) é uma função R em R, onde para todo t leva-se ao valor g(t), pela lei g(t) = f(2cost, sent), g eh uma composta!
Existe uma função h(t) intermediária, tal que para cada valor de t, eh associado a um h(t) = ( 2cost, sent)
Dessa forma, minha g(t) nada mais é do que uma f(h(t)).
Nesta função x = x(t) e y = y(t)
Acredito que a regra da cadeira será dada por:
dg/dt = df/dx dx/dt + df/dx dy/dt
Podemos determinar dx/dt = d(2cos(t))/dt = - 2 sen(t)
Podemos determinar dy/dt = d(sent)/dt = cos(t)
Assim,
dg/dt = -2 sent df/dx + cost df/dy
Também vamos lembrar que temos por hipotese que 4y. df/dx (x,y) - x df/dy(x,y) = 2
Mas não consigo unir as duas equações!!!
Falta algum dado?


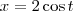 e
e 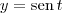 , então:
, então: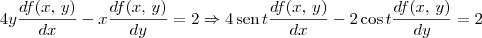
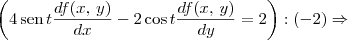
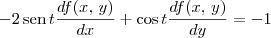
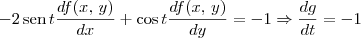

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)